Завдання: У прямокутній системі координат на площині xy задано точки O(0;0) і A(6;8). З точки A на вісь X опущено перпендикуляр. Точка B – основа цього перпендикуляра. Установіть відповідність між величиною (1-4) та її числовим значенням (А-Д)
$$\begin{array}{|l|c|} \hline \\ Величина & Числове \quad значення \\ \hline \\ 1.\quad довжина \quad вектора \quad OA & А \quad 0 \\ \hline \\ 2.\quad відстань \quad від \quad точки\quad A\quad до\quad осі\quad x & Б \quad 5 \\ \hline \\ 3.\quad ордината\quad точки\quad B & В\quad 6 \\ \hline \\ 4.\quad довжина\quad радіуса\quad кола,\quad описаного\quad навколо\quad трикутника\quad OAB\quad & Г\quad 8 \\ \hline \\ & Д\quad 10 \\ \hline \end{array}$$
Рішення: нарисуем декартовую систему координат и нанесем на нее точки, согласно условия задачи
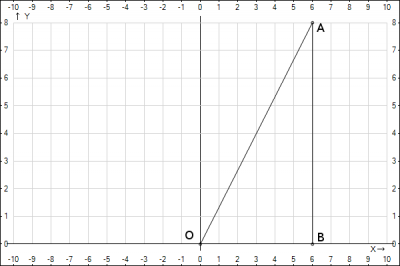
рисунок позволит нам ответить на все вопросы задания.
1. Длина вектора OA, рассчитывается по формуле \(r = \sqrt{(x_A-x_O)^2 + (y_A-y_O)^2}\) - формула длины отрезка в декартовой системе координат или находим длины катетов прямоугольного треугольника ΔOAB, а длину гипотенузы \(OA\) находим по теореме Пифагора \(OA = \sqrt{OB^2 + AB^2}\). Подставляем данные в формулу $$OA = \sqrt{6^2+8^2} = 10$$
Відповідь: \(1 =>Д - 10 \)
2. Расстояние от точки A до оси x - значение координаты \(y = 8\) точки A.
Відповідь: \(2 =>Г - 8 \)
3. Ордината точки B. Помним, что в декартовой системе координат координаты точки называются x - абсцисса, а y - ордината, т.о ордината точки B: y = 0
Відповідь: \(3 =>А - 0 \)
4. Длина радиуса круга, описанного вокруг треугольника ΔOAB. Помним, что центр круга, описанного около прямоугольного треугольника лежит на его гипотенузе, которая является его диаметром, т.е. \(r = \frac{OA}{2} = \frac{10}{2} = 5\)
Відповідь: \(4 =>Б - 5 \)
