ЗНО 2013 року з математики (1 сесія). Завдання № 20.

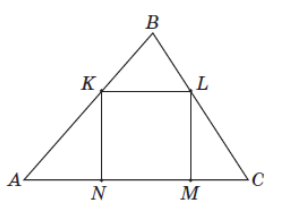
Завдання: У трикутник ABC вписано квадрат KLMN (див.рисунок). Висота цього трикутника, проведена до сторони AC, дорівнює 6 см. Знайдіть периметр квадрата, якщо AC =  10 см.

$$\begin{array}{|c|c|c|с|c|} \hline \\ А & Б &  В &  Г &  Д \\ \hline  \\ 15 cm &  7,5 cm &  12,5cm & 17,5cm & 20cm\\ \hline \end{array}$$

Рішення: нанесем на рисунок высоту и обозначим точки пересечения высоты со стороной треугольника AC (точка D) и стороной квадрата KL (точка E).

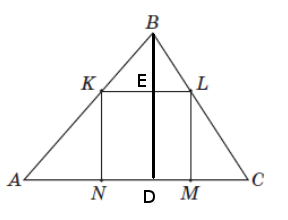
Рассмотрим два треугольника ΔABC и ΔKBL эти треугольники подобны по двум углам, т.к. сторона KL параллельна стороне AC, т.к. на стороне AC лежит сторона MN квадрата, а как известно сторона квадрата параллельны MN || KL, тогда прилежащие к этим сторонам углы равны $\angle BAC = \angle BKL$ и $\angle BCA = \angle BLK$. Составим пропорцию

$$\frac{KL}{AC} = \frac{BE}{BD} =>$$ обозначим сторону квадрата за $a = KL=LM=MN=NK$, тогда $BE = BD - ED => BE = 6 - a$ подставим полученные значения в формулу $$\frac{a}{10} = \frac{6-a}{6} => 6a = 60-10a => 16a=60 => a = \frac{15}{4}$$ Как известно, периметр квадрата равен $P=4a$. подставляем в периметр подученное значение длины стороны $$P = 4a = 4*\frac{15}{4} = 15$$

Відповідь: $A -> 15 cm$

 наступне завдання № 22