Рассмотрим принцип решения задач по теме : "Прямая линия на плоскости, нахождение уравнения прямой, проходящей через заданную точку, нахождение точек пересечения, углов биссектрис и т.д.".
В качестве примера рассмотрим следующую задачу
Пример: Даны координаты вершин треугольника \(ABC\) \(A(3; -3); B(-1;-6); C(-6;0)\)
- Составьте уравнение сторон треугольника.
- Найдите уравнение
- высоты \(AD\),
- медианы \(BM\),
- биссектрисы \(CF\).
- Составьте систему неравенств, областью решения которой является множество всех точек треугольника \(ABC\).
- Найдите угол \(B\) в радианах с точностью до двух знаков.
- Сделайте чертеж.
Решение:
- Составьте уравнение сторон треугольника. Для составления уравнения сторон треугольника обратимся к условию задачи. В условии даны координаты трех вершин треугольника, т.е. для составления уравнения прямых \(AB,BC,CD\) даны по 2 точки, через которые эти прямые проходят. Для решения воспользуемся уравнением прямой, проходящей через две заданные точки $$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$$ где \((x_1;y_1)\) - координаты первой известной точки, \((x_2;y_2)\) - координаты второй известной точки. Подставим координаты и получим уравнение прямых
прямая \(AB\) , проходит через точки \(A(3; -3); B(-1;-6)\), составим уравнение $$\frac{y-(-3)}{(-6)-(-3)}=\frac{x-3}{-1-3} =>\frac{y+3}{-3}=\frac{x-3}{-4} =>y=\frac{3}{4}x-\frac{21}{4}$$ получили уравнение прямой \(AB\). В уравнении прямой отметим угловой коэффициент \(k_{AB} = \frac{3}{4}\), который понадобится в следующих задачах.
прямая \(BC\), проходит через точки \(B(-1;-6);C(-6;0)\), составим уравнение $$\frac{y-(-6)}{0-(-6)}=\frac{x-(-1)}{-6-(-1)} =>\frac{y+6}{6}=\frac{x+1}{-5} =>y=-\frac{6}{5}x-\frac{36}{5}$$ получили уравнение прямой \(BC\). В уравнении прямой отметим угловой коэффициент \(k_{BC} = -\frac{6}{5}\), который понадобится в следующих задачах.
прямая \(AC\), проходит через точки \(A(3; -3);C(-6;0)\), составим уравнение $$\frac{y-(-3)}{0-(-3)}=\frac{x-3}{-6-3} =>\frac{y+3}{3}=\frac{x-3}{-9} =>y=-\frac{1}{3}x-2$$ получили уравнение прямой \(AC\). В уравнении прямой отметим угловой коэффициент \(k_{AC} = -\frac{1}{3}\), который понадобится в следующих задачах. - Найдите уравнение
- высоты \(AD\), в уравнении высоты у нас известна координата только одной точки - \(A(3; -3)\), поэтому воспользуемся уравнением прямой, проходящей через заданную точку в данном направлении. $$y-y_0=k_{AD}(x-x_0)$$ , где \((x_0;y_0)\) - координаты известной точки, а \(k_{AD}\) - угловой коэффициент. В данном уравнении нам неизвестен только угловой коэффициент. Найдем его, для этого воспользуемся свойство перпендикулярных прямых. Прямая \(AD \bot BC\). Запишем свойство \(k_{AD}*k_{BC} = -1 =>k_{AD}*( -\frac{6}{5})= -1 =>k_{AD}=\frac{5}{6}\). Составим уравнение прямой \(AD\) $$y-(-3)=\frac{5}{6}(x-3)=>y = \frac{5}{6}x-\frac{11}{2}$$
- медианы \(BM\), для нахождения уравнения медианы в задаче даны координаты одной точки \(B(-1;-6)\), а также известно, что медиана делит противоположную сторону пополам. Найдем координаты точки \(M\). Для этого воспользуемся формулой координаты точки, которая делит отрезок \(AC\) в заданном отношении \(\lambda\), где \(\lambda = \frac{AM}{MC}=\frac{1}{1}=1\), а координаты \((x_1;y_1),(x_2;y_2)\) - координаты концов отрезка, который делит точка \(M\) т.е.точек \(A(3; -3); C(-6;0)\), подставим и получим $$x = \frac{x_1+\lambda x_2}{1+\lambda}=\frac{3+1*(-6)}{1+1}=-\frac{3}{2}$$$$y = \frac{y_1+\lambda y_2}{1+\lambda}=\frac{-3+1*0}{1+1}=-\frac{3}{2}$$получили координаты точки \(M(-\frac{3}{2};-\frac{3}{2})\). Получили две точки, через которые проходит прямая, для получения уравнения прямой воспользуемся уравнением прямой, проходящей через заданные две точки \(\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}\), подставим координаты точек \( B(-1;-6),M(-\frac{3}{2};-\frac{3}{2}) \) и получим $$\frac{y+6}{-\frac{3}{2}+6}=\frac{x+1}{-\frac{3}{2}+1} =>y=-9x-15$$
- биссектрисы \(CF\), для нахождения уравнения биссектрисы воспользуемся свойством биссектрисы угла треугольника: биссектриса внутреннего угла треугольника делит противоположную углу сторону на отрезки, пропорциональные двум другим сторонам \(\frac{AF}{FB}=\frac{AC}{BC}\), т.е. таким образом мы найдем коэффициент \(\lambda\), затем воспользуемся формулой координаты точки, которая делит отрезок \(AB\) в заданном отношении \(\lambda\) и найдем координаты точки \(F\) и последнее, подставим полученные координаты в уравнение прямой, проходящей через две заданные точки.
Приступим: найдем длины отрезков \(AC\), \(BC\). $$AC = \sqrt{(x_c-x_a)^2+(y_b-y_a)^2}=\sqrt{(-6-3)^2+(0-(-3))^2} =\sqrt{9^2+3^2}=\sqrt{90}$$$$BC = \sqrt{(x_c-x_b)^2+(y_c-y_b)^2}=\sqrt{(-6-(-1))^2+(0-(-6))^2} =\sqrt{5^2+6^2}=\sqrt{61}$$ теперь найдем коэффициент \(\lambda=\frac{AF}{FB}=\frac{AC}{BC}=\sqrt{\frac{90}{61}}\). Найдем координаты точки \(F\) при известных координатах концов отрезка \(AB\) \(A(3; -3); B(-1;-6)\) $$x = \frac{x_1+\lambda x_2}{1+\lambda}=\frac{3-\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}}$$$$y = \frac{y_1+\lambda y_2}{1+\lambda}=\frac{-3-6*\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}}$$Получили две точки, через которые проходит прямая \(CF\), для получения уравнения прямой \(CF\) воспользуемся уравнением прямой, проходящей через заданные две точки \(\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}\), подставим координаты точек \( C(-6;0); F(\frac{3-\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}};\frac{-3-6*\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}}) \) и получим $$\frac{y-0}{\frac{-3-6*\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}}-0}=\frac{x+6}{\frac{3-\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}}+6} =>\frac{y}{\frac{-3-6*\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}}}=\frac{x+6}{\frac{3-\sqrt{\frac{90}{61}}+6+6*\sqrt{\frac{90}{61}}}{1+\sqrt{\frac{90}{61}}}} =>$$$$\frac{y}{-3-6*\sqrt{\frac{90}{61}}}=\frac{x+6}{9+5\sqrt{\frac{90}{61}}}=>$$$$y=\frac{x+6}{9+5\sqrt{\frac{90}{61}}}*(-3-6*\sqrt{\frac{90}{61}})=>$$$$y=-\frac{3+6*\sqrt{\frac{90}{61}}}{9+5\sqrt{\frac{90}{61}}}*x-18\frac{1+2*\sqrt{\frac{90}{61}}}{9+5\sqrt{\frac{90}{61}}}$$ - Составьте систему неравенств, областью решения которой является множество всех точек треугольника \(ABC\). Это множество точек, которые лежат ниже прямой \(AC\), т.е. \(y \leq -\frac{1}{3}x-2\), выше прямых \(BC\) \(y \geq -\frac{6}{5}x-\frac{36}{5}\) и \(AB\) \(y \geq \frac{3}{4}x-\frac{21}{4}\), запишем это $$\begin{cases}y \leq -\frac{1}{3}x-2 \\ y \geq -\frac{6}{5}x-\frac{36}{5} \\ y \geq \frac{3}{4}x-\frac{21}{4} \end{cases}$$
- Найдите угол \(B\) в радианах с точностью до двух знаков. Угол между прямыми рассчитывается по формуле $$\mbox{tg}a = |\frac{k_2-k_1}{1+k_1*k_2}|$$где \(k_1=k_{BC}=-\frac{6}{5}\), \(k_2=k_{AB}=\frac{3}{4}\) подставим в формулу $$\mbox{tg}a = |\frac{\frac{3}{4}+\frac{6}{5}}{1-\frac{3}{4}*\frac{6}{5}}|=19\frac{1}{2} => a = 87.06^0$$Данная формула позволяет вычислить острый угол между прямыми. Из рисунка видно, что искомый угол \(B\) треугольника - тупой угол \(ΔADB\) - прямоугольный, угол \(D=90\), остальные два угла в сумме меньше \(90^0\), т.е. \(B = 180^0-a=180^0-87.06^0=92,94^0\). В задаче необходимо в ответе указать угол в радианах \(B=92,94^0*\frac{\pi}{180^0}=1,62\)
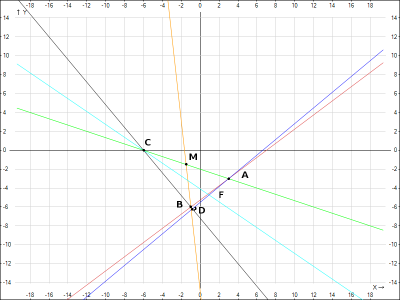
- Сделайте чертеж.