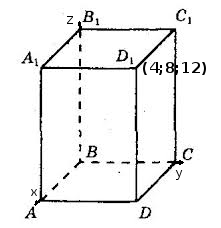
Завдання: У прямокутній системі координат у просторі зображено прямокутний паралелепіпед \(ABCDA_1B_1C_1D_1\), ребра \(AB\), \(BC\), \(BB_1\) якого лежать на координатних осях (див. рисунок). Вершина \(D_1\) має координати (4;8;12). До кожного початку речення (1-4) доберіть його закінчення (А-Д) так, щоб утворилося правильне твердження.
Початок речення
- Точка \(K(0;0;12)\)
- Точка \(M(1;8;0)\)
- Точка \(P(4;4;4)\)
- Точка \(Q(0;4;6)\)
Закінчення речення
А належить грані \( AA_1D_1D \)
Б належить ребру \( CD \)
В належить діагоналі \( AC_1 \)
Г належить діагоналі \( BC_1 \)
Д збігається з точкою \( B1 \)
Теорія до завдання: рассмотрим основные моменты, используя которые можно просто решить данный тип задач. Все ребра и плоскости перпендикулярны.
- Точка, ребро лежит на оси. Если точка лежит на оси, например \(x\) , то все ее координаты кроме этой оси равны 0. Рассмотрим наш случай. На оси \(x\) лежит точка \(A\), т.е. ее координаты \((x;0;0)\). Как определить \(x\). Есть на рисунке только 1 точка с координатами - точка \(D_1(4;8;12)\). Т.е. у нас прямоугольный параллелепипед, то точка \(A\) - проекция точки \(D_1\) на ось \(x\), т.е. координата \(A(4;0;0)\). Соответственно \(C(0;8;0)\), \(B_1(0;0;12)\).
Если точка лежит на ребре, то соответственно смотрим на какой оси лежит ребро, т.е. определяем нулевые координаты, а величина ненулевой координаты координаты должна попадать диапазон от начала координат до вершины, т.е. , например,если точка лежит на ребре \(AB\) ее координаты должны быть \( (0 < x < 4; 0; 0) \) - Точка лежит на грани. Если точка лежит на грани, смотрим в какой плоскости лежит грань, если в координатной плоскости, например, \(xz\), то координата \(y=0\), т.е. ее координаты \( (0 < x < 4; 0 < y < 8; 0) \)
Рішення:
- Точка \(K(0;0;12)\) - координаты \(x=0; y=0\), т.е эта точка лежит на оси \(z\), а так как ее координата \(z =12\),то точка \(K\) совпадает с вершиной \(B_1\) (см. Теорія до завдання 1)
Відповідь: 1 -->Д - Точка \(M(1;8;0)\). Координата точки \(z=0\), т.е. эта точка лежит в плоскости \(xy\), т.е. \( (x=1 < 4 ; y = 8 ; 0) \)
точка лежит на ребре \(CD\)
Відповідь: 2 -->Б - Точка \(P(4;4;4)\). У точки все три координаты, при этом \( x = 4; y = 4 < 8 ; z = 4 < 12\). \( x = 4\) означает, что точка лежит в плоскости перпендикулярной оси \( x \) в точке \( x=4 \), попадание \( y \) и \( z \) в диапазон \( y = 4 < 8 ; z = 4 < 12\) означает, что она лежит на грани \(AA_1D_1D\).
Відповідь: 3 -->А - Точка \(Q(0;4;6)\). Координата \(x = 0\) означает, что точка лежит в плоскости \(yz\). Рассмотрим остальные координаты \(y = 4 < 8, z = 6 < 12\), т.е. точка лежит на грани \(BB_1C_1C\). Проверим лежит ли она на диагонали \(BC_1\). Координата точки \(C_1(0;8;12)\). Тангенс угла наклона диагонали к оси \(y\) равен \(tg = k = \frac{12}{8} = \frac{3}{2}\) отсюда получим уравнение прямой, на которой лежит диагональ \(z = \frac{3}{2}y\). Если подставить координаты точки в это уравнение и получится истинное равенство, то точка \(Q(0;4;6)\) лежит на диагонали. Подставим \( z = \frac{3}{2}y => 6 = \frac{3}{2} 4 =>6=6\). Вывод, точка \(Q(0;4;6)\) лежит на диагонали \( BC_1 \).
Відповідь: 4 -->Г
Відповідь:
1 -->Д
2 -->Б
3 -->А
4 -->Г

