Завдання: Кожній функції (1-4) поставте у відповідність координатні чверті (А-Д), у яких розміщено графік функції.
Функція
- \(y = x+1\)
- \( y = \frac{1}{x}\)
- \(y = 2^x\)
- \(y = x^2-1\)
Координатні чверті
А ----лише І та ІІ.
Б ----лише І та ІІІ.
В ----лише І, ІІ та ІІІ.
Г ----лише І, ІІІ та ІV.
Д ----І,ІІ,ІІІ та ІV.
Рішення: это задание на знание графиков элементарных функций и их
- \(y = x+1\) - график элементарной функции прямой \(y = x\) (является биссектрисой І и ІІІ четверти на рисунке красная, т.е. при x > 0, y>0, при x < 0, y < 0), полученный путем параллельного переноса графика \(y = x\) вдоль оси \(y \) вверх на 1. Т.е. функция \( y = x \) проходила через І и ІІІ четверти, то после переноса будет проходить через І,ІІ,ІІІ четверти.
Відповідь: 1 -->В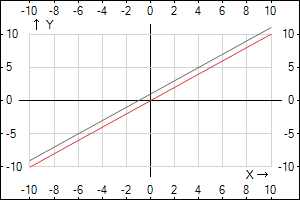
- \( y = \frac{1}{x}\) - график элементарной функции гиперболы, из уравнения видно, что при x>0 , y>0, при x<0, y<0, т.е. график функции проходит через І и ІІІ четверти.
Відповідь: 2 -->Б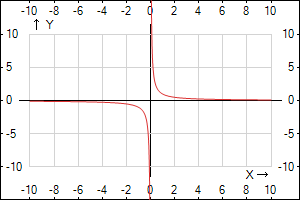
- \(y = 2^x\) это график показательной функции, мы помним, что при любых \(x \in (-\infty; +\infty)\) \(y>0\), т.е. график функции проходит через І и ІІ четверти.
Відповідь: 3 -->А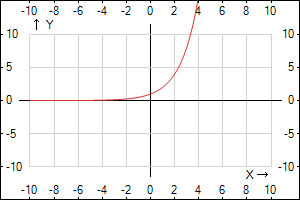
- \(y = x^2-1\) - график функции полученный из графика функции \(y= x^2 \) (это парабола, при всех \(x \in (-\infty; +\infty) \)\(y>0\)) путем переноса на 1 вниз вдоль оси \( y\), т.е. если исходная парабола была в І и ІІ четверти, то после перенос на 1 вниз она будет в І, ІІ, ІІІ, ІV четвертях
Відповідь: 4 -->Д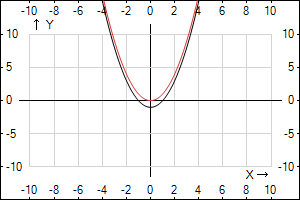
Відповідь:
1 -->В
2 -->Б
3 -->А
4 -->Д

