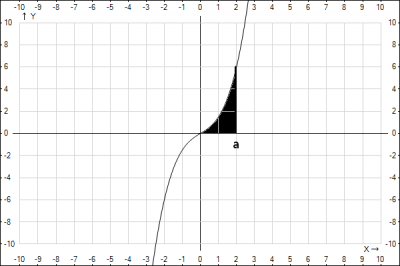
Завдання: У прямокутній системі координат зображено ескіз графіка функції \( y = \frac{x^3}{2} + x\) і пряму, задану рівнянням \( x=a \) (див. рисунок). При якому додатному значенні \( a\) площа заштриховано фігури дорівнюватиме 40 кв.од.?
Рішення: вспомним геометрический смысл определенного интеграла - площадь фигуры ограниченной сверху графиком функции, снизу осью \(x\), а справа и слева перпендикулярами к оси \(x\). Это определение практически полностью заложено в задании. Т.о. ищем определенный интеграл $$S =\int_0^a ( \frac{x^3}{2} + x) dx =$$применим свойство интеграла - интеграл суммы равен сумме интегралов \( \int (f(x) +g(x)) dx = \int f(x) dx + \int g(x) dx\) , а также формулу Ньютона — Лейбница или ее еще называют основная формула интегрального исчисления \(\int_a^b f(x) dx = F(x) |_a^b = F(b) - F(a)\), где \(a \) - левая граница искомой площади, в нашем случае \(a = 0\), а \(b\) - правая граница искомой площади, в нашем случае - неизвестная \( a \). Применим указанные формулы и значения границ и получим$$S =\int_0^a \frac{x^3}{2}\, dx + \int_0^a x \, dx =$$ получили два табличных интеграла степенной функции, он равен \( \int x^a \,dx = \frac{a^{a+1}}{a+1} + C\). Подставим в нашу формулу и учтем формулу Ньютона — Лейбница $$= \frac{x^{3+1}}{2(3+1)} + \frac{x^{1+1}}{1+1} |_0^a = \frac{x^4}{8} + \frac{x^2}{2} |_0^a = \frac{a^4}{8} + \frac{a^2}{2} - (\frac{0^4}{8} + \frac{0^2}{2}) = \frac{a^4}{8} + \frac{a^2}{2}$$интеграл (площадь фигуры) мы нашли, теперь нужно найти значение \(a \). Для этого воспользуемся второй частью условия, где говорится что площадь равна 40 ед. кв.. Приравняем и получим уравнение четвертой степени и решим его $$ \frac{a^4}{8} + \frac{a^2}{2} = 40 =>a^4 + 4a^2 - 320 = 0$$это уравнение можно рассматривать как квадратное относительно \(a^2\), для тех кто не увидел, сделаем замену \(t = a^2\), подставим $$t^2 + 4t^2 - 320 = 0 =>$$$$ t_{1,2} = \frac{-4 \pm \sqrt{16 + 3* 320}}{2} = \frac{-4 \pm \sqrt{1296}}{2} = \frac{-4 \pm 36}{2}$$получили следующие корни \( a^2 =t_{1} = 16\), \( a^2 =t_{2} = -20\), т.к. квадрат может быть только положительным, то получаем $$ a^2 = 16 => a = \pm 4$$ согласно условия задачи параметр \(a\) - положительное число, поэтому оставляем одно значение \(a = 4\)
Відповідь: 4.
попереднє завдання № 30 наступне завдання № 32

