Завдання: У прямокутній трапеції \(ABCD\) (AD||BC) діагональ \(AC\) перпендикулярна до бічної сторони \(CD\). Знайдіть довжину цієї діагоналі (у см), якщо \(AD = 18 cm\), \( DC = 8cm\).
Рішення: нарисуем рисунок
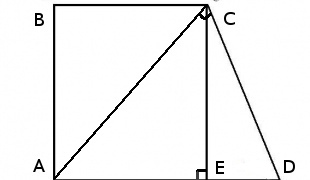
Опустим из вершины \(C\) перпендикуляр на основание \( AD\)в точку \(E\). Обозначим \( AB = CE = x\), \( CD = y\), а диагональ, которую необходимо найти \( AC = z\). Рассмотрим три прямоугольных треугольника \(ΔACE, ΔECD, ΔACD\), запишем для каждого из них теорему Пифагора и составим систему уравнений $$\begin{cases} AE^2+CE^2 = AC^2\\ CE^2+ED^2=CD^2 \\ CD^2 +AC^2 = AD^2 \end{cases} =>$$подставим замену и известные длины из условия задачи \(BC = AE = 8\), \(AD = 18\), учтем, что \(ED = AD - AE = 18 - 8 = 10\)
$$\begin{cases} 8^2+x^2 = z^2\\ x^2+10^2 = y^2 \\ y^2 +z^2 = 18^2 \end{cases} =>\begin{cases} 8^2+x^2 = z^2\\ x^2 = y^2 - 10^2 \\ y^2 = 18^2 - z^2 \end{cases} =>$$$$\begin{cases} 8^2+18^2 - z^2 - 10^2 = z^2\\ x^2 = 18^2 - z^2 - 10^2 \\ y^2 = 18^2 - z^2 \end{cases} $$ получили уравнение одной неизвестной, которое необходимо решить, остальные неизвестные искать нет необходимости $$z^2 = 8^2+18^2 - z^2 - 10^2 => 2z^2 = 64+18^2 - 100 => $$$$z =\sqrt{\frac{18^2 - 36}{2}} => z =\sqrt{18*9 - 18} =>$$$$z =\sqrt{18(9 - 1)} => z =\sqrt{18*8} => z =\sqrt{(3*3*2)*(2*2*2)} =>$$$$z=12$$Відповідь: 12
попереднє завдання № 29 наступне завдання № 31

