Завдання: При якому значенні \( x \) функція \( y = 4-|20x+7|\) набуває найбільшого значення.
Рішення: Раскроем модуль и получим следующую систему
$$y = \left[ \begin{gathered} \begin{cases} 4-20x-7 \\ 20x+7 \geq 0 \end{cases} \\ \begin{cases} 4+20x+7 \\ 20x+7 < 0 \end{cases} \end{gathered}\right.=>\left[ \begin{gathered} \begin{cases} -3-20x \\ x \geq -\frac{7}{20} \end{cases} \\ \begin{cases} 11+20x \\ x < -\frac{7}{20} \end{cases} \end{gathered}\right.$$Для наглядности построим график
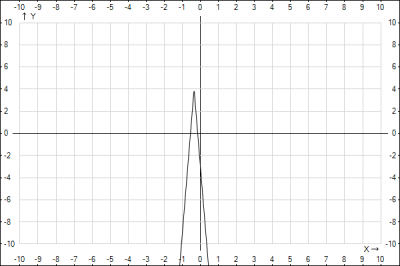
На рисунке видно, что функция принимает наибольшее значение при \(x = -\frac{7}{20} = -0,35\)
Відповідь: -0,35
попереднє завдання № 25 наступне завдання № 27

