–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –≥—А–∞—Д–Є–Ї–∞ —Д—Г–љ–Ї—Ж–Є–Є –љ–∞ —Б–ї–µ–і—Г—О—Й–µ–Љ –њ—А–Є–Љ–µ—А–µ:
–Я—А–Є–Љ–µ—А: –Я–Њ—Б—В—А–Њ–Є–Љ—В—М –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є \( x \to y(x)\), –Ј–∞–і–∞–љ–љ–Њ–≥–Њ –љ–µ—П–≤–љ–Њ, –њ–∞—А–∞–Љ–µ—В—А —Б—З–µ—В–∞—В—М –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ—Л \( a > 0\). $$x^4 + y^4 = a^2 (x^2 + y^2)$$
–†–µ—И–µ–љ–Є–µ: –њ—А–Њ–≤–µ–і–µ–Љ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ –≥—А–∞—Д–Є–Ї–∞ —Д—Г–љ–Ї—Ж–Є–Є –Є –њ–Њ—Б—В—А–Њ–Є–Љ –µ–≥–Њ –њ–Њ —Е–∞—А–∞–Ї—В–µ—А–љ—Л–Љ —В–Њ—З–Ї–∞–Љ. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є —Б–Є–Љ–Љ–µ—В—А–Є—З–µ–љ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Њ—Б–µ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В.–µ. –µ—Б—В—М –±—Г–і–µ–Љ –њ—А–Њ–≤–Њ–і–Є—В—М –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ –≥—А–∞—Д–Є–Ї–∞ –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—А—В–Є, —В.–µ. –њ—А–Є \( x \geq 0\) –Є \( y \geq 0\). –§—Г–љ–Ї—Ж–Є—П –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –Є –љ–µ–њ—А–µ—А—Л–≤–љ–∞ –њ—А–Є –≤—Б–µ—Е \( x\). –Я—А–µ–і—Б—В–∞–≤–Є–Љ –Ї—А–Є–≤—Г—О –≤ –њ–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–Љ –≤–Є–і–µ, –Ј–∞–Љ–µ–љ–Є–Љ \( y = tx\). –Ґ.–Ї. –Љ—Л —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ –Ї—А–Є–≤—Г—О –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—В–Є, —В–Њ \( y \geq 0\). –Я–Њ–і—Б—В–∞–≤–Є–Љ $$x^4 + y^4 = a^2 (x^2 + y^2) => x^4 + (tx)^4 = a^2 (x^2 + (tx)^2) =>$$$$x^2 + t^4x^2 = a^2 (1 + t^2) =>x^2 = a^2 \frac{1 + t^2}{ 1+ t^4} = x = a \sqrt{ \frac{1 + t^2}{ 1+ t^4}}$$ –њ–Њ–і—Б—В–∞–≤–Є–Љ –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П \( y \) $$ y = tx => y = t a \sqrt{ \frac{1 + t^2}{ 1+ t^4}}$$ –Т—Л—З–Є—Б–ї–Є–Љ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ \( x' \) –Є \( y' \) $$x' = (a \sqrt{ \frac{1 + t^2}{ 1+ t^4}})'=\frac{a}{2}\sqrt{\frac{ 1+ t^4}{1 + t^2}}\frac{2t(1 + t^4)-4t^3(1 + t^2)}{(1 + t^4)^2}' = a \sqrt{\frac{ 1+ t^4}{1 + t^2}}\frac{t(1 - 2t^2 -t^4 )}{(1 + t^4)^2}$$ –њ—А–Є—А–∞–≤–љ—П–µ–Љ –њ–µ—А–≤—Г—О –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О –Ї 0 –Є –љ–∞–є–і–µ–Љ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–µ —В–Њ—З–Ї–Є $$x' = a \sqrt{\frac{ 1+ t^4}{1 + t^2}}\frac{t(1 - 2t^2 -t^4 )}{(1 + t^4)^2} =0 => t(1 - 2t^2 -t^4 ) = 0 => t_1 = 0, t_2=¬† \sqrt{\sqrt2 -1}$$ –Њ–њ—А–µ–і–µ–ї—П–µ–Љ –Ј–љ–∞–Ї –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –≤ –Њ–Ї—А–µ—Б–љ–Њ—Б—В–Є —Н—В–Є—Е —В–Њ—З–µ–Ї, –њ–Њ–ї—Г—З–Є–Љ
- –≤ —В–Њ—З–Ї–µ \( t = 0; x = a; y=0\) –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –Љ–µ–љ—П–µ—В –Ј–љ–∞–Ї —Б - –љ–∞ + —В.–µ. —Н—В–Њ —В–Њ—З–Ї–∞ –Љ–Є–љ–Є–Љ—Г–Љ–∞
- –≤ —В–Њ—З–Ї–µ \( t =¬† \sqrt{\sqrt2-1}; x = a\sqrt{\frac{\sqrt2 + 1}{2}}; y = \frac{1}{\sqrt2}\) –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –Љ–µ–љ—П–µ—В –Ј–љ–∞–Ї —Б + –љ–∞ - —В.–µ. —Н—В–Њ —В–Њ—З–Ї–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞
–њ—А–Њ–≤–µ–і–µ–Љ –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ –Є —Б –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є \( y \)
$$y' = (at \sqrt{ \frac{1 + t^2}{ 1+ t^4}})'=(a \sqrt{ \frac{t^2 + t^4}{ 1+ t^4}})'= a \frac{1}{2} \sqrt{ \frac{1+ t^4}{t^2 + t^4}}*\frac{(2t+4t^3)(1+ t^4)-4t^3(1 + t^4)}{(1+ t^4)^2} = $$$$ =¬† a \frac{1}{t} \sqrt{ \frac{1+ t^4}{1 + t^2}}*t*\frac{1+2t^2-t^4}{(1+t^4)^2}=¬† a¬† \sqrt{ \frac{1+ t^4}{1 + t^2}}\frac{1+2t^2-t^4}{(1+t^4)^2}$$ –њ—А–Є—А–∞–≤–љ—П–µ–Љ –њ–µ—А–≤—Г—О –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О –Ї 0 –Є –љ–∞–є–і–µ–Љ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–µ —В–Њ—З–Ї–Є $$y' = a \sqrt{ \frac{1+ t^4}{1 + t^2}}\frac{1+2t^2-t^4}{(1+t^4)^2} =0 => 1+2t^2-t^4 = 0 =>¬† t=¬† \sqrt{\sqrt2 +1}$$ –Њ–њ—А–µ–і–µ–ї—П–µ–Љ –Ј–љ–∞–Ї –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –≤ –Њ–Ї—А–µ—Б–љ–Њ—Б—В–Є —Н—В–Є—Е —В–Њ—З–µ–Ї, –њ–Њ–ї—Г—З–Є–Љ
–њ–Њ–ї—Г—З–Є–ї–Є, —З—В–Њ –≤ —В–Њ—З–Ї–µ \( t =¬†¬† \sqrt{\sqrt2 +1}; x = a \frac{1}{\sqrt2}; y = a \sqrt{\frac{\sqrt2+1}{2}} \) –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –Љ–µ–љ—П–µ—В –Ј–љ–∞–Ї —Б + –љ–∞ - —В.–µ. —Н—В–Њ —В–Њ—З–Ї–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞
–љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М —В–Њ—З–Ї—Г –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \( y \), —Б –Њ—Б—М—О \( x \) —Г–ґ–µ –µ—Б—В—М - —Н–Ї—Б—В—А–µ–Љ—Г–Љ. \( x=0, x^4 + y^4 = a^2 (x^2 + y^2) => y^4 = a^2y^2 => y =a\)
–Ґ.–Њ. –њ–Њ–ї—Г—З–Є–і–ї–Є —Б–ї–µ–і—Г—О—Й–Є–µ —В–Њ—З–Ї–Є:
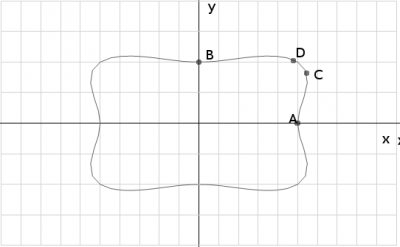
\(A:(x = a; y=0)\)¬† —В–Њ—З–Ї–∞ –Љ–Є–љ–Є–Љ—Г–Љ–∞
\(B:(x = 0; y=a)\)¬† —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \( y \)
\(C:(x = a\sqrt{\frac{\sqrt2 + 1}{2}}; y = \frac{1}{\sqrt2})\)¬† —В–Њ—З–Ї–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ –њ–Њ \( x \)
\(D:(x = a \frac{1}{\sqrt2}; y = a \sqrt{\frac{\sqrt2+1}{2}}) \)¬† —В–Њ—З–Ї–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ –њ–Њ \( y \)
–Э–∞–љ–µ—Б–µ–Љ —Г–Ї–∞–Ј–∞–љ–љ—Л–µ —В–Њ—З–Ї–Є –љ–∞ –і–µ–Ї–∞—А—В–Њ–≤—Г—О —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞–Љ, –њ–Њ—Б—В—А–Њ–Є–Љ –Ї—А–Є–≤—Г—О –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—В—А–Є, –Ј–∞—В–µ–Љ —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ –Њ—В–Њ–±—А–∞–Ј–Є–Љ –µ–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Њ—Б–Є \( Ox\), –Ј–∞—В–µ–Љ \(Oy\) –Є –њ–Њ–ї—Г—З–Є–Љ —Б–ї–µ–і—Г—О—Й–Є–є —А–µ—Й—Г–ї—М—В–∞—В