–Ч–Љ—Ц—Б—В –Ј–∞–≤–і–∞–љ–љ—П: –Ю—Б–љ–Њ–≤–Њ—О –њ—А—П–Љ–Њ—Ч –њ—А–Є–Ј–Љ–Є \(ABCDA_{1}B_{1}C_{1}D_{1}\) —Ф —А—Ц–≤–љ–Њ–±—Ц—З–љ–∞ —В—А–∞–њ–µ—Ж—Ц—П \(ABCD\). –Ю—Б–љ–Њ–≤–∞ \(AD\) —В—А–∞–њ–µ—Ж—Ц—Ч –і–Њ—А—Ц–≤–љ—О—Ф –≤–Є—Б–Њ—В—Ц —В—А–∞–њ–µ—Ж—Ц—Ч —Ц –≤ —И—Ц—Б—В—М —А–∞–Ј—Ц–≤ –±—Ц–ї—М—И–∞ –Ј–∞ –Њ—Б–љ–Њ–≤—Г \(BC\). –І–µ—А–µ–Ј –±—Ц—З–љ–µ —А–µ–±—А–Њ \(CC_{1}\) –њ—А–Є–Ј–Љ–Є –њ—А–Њ–≤–µ–і–µ–љ–Њ –њ–ї–Њ—Й–Є–љ—Г –њ–∞—А–∞–ї–µ–ї—М–љ–Њ —А–µ–±—А—Г \(AB\). –Ч–љ–∞–є–і—Ц—В—М –њ–ї–Њ—Й—Г —Г—В–≤–Њ—А–µ–љ–Њ–≥–Њ –њ–µ—А–µ—А—Ц–Ј—Г (—Г \(—Б–Љ^2\)), —П–Ї—Й–Њ –Њ–±вАЩ—Ф–Љ –њ—А–Є–Ј–Љ–Є –і–Њ—А—Ц–≤–љ—О—Ф 672 \(—Б–Љ^3\), –∞ —Ч—Ч –≤–Є—Б–Њ—В–∞ вАФ 8 —Б–Љ.
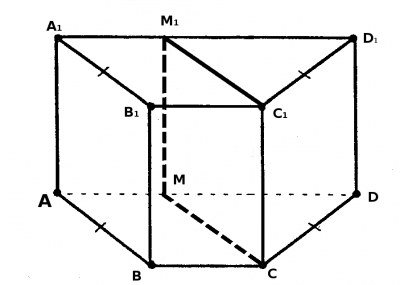
–†—Ц—И–µ–љ–љ—П: –Я–Њ–Ј–љ–∞—З–Є–Љ–Њ —И—Г–Ї–∞–љ–Є–є —А–Њ–Ј—А—Ц–Ј —П–Ї \(CC_ {1}M_{1}M\) , —Г —А–Њ–Ј—А—Ц–Ј—Ц –Љ–Є –Њ—В—А–Є–Љ–∞–ї–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–Ї, —В–Њ–Љ—Г —Й–Њ –њ–ї–Њ—Й–Є–љ–∞ –њ—А–Њ—Е–Њ–і–Є—В—М —З–µ—А–µ–Ј —А–µ–±—А–Њ \(CC_1\), –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ –≤–Њ–љ–∞ —В–∞–Ї–Њ–ґ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –Њ—Б–љ–Њ–≤–∞–Љ. –Я–ї–Њ—Й–∞ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–Ї–∞ –і–Њ—А—Ц–≤–љ—О—Ф \(S = CC_1 * CM\). –°—В–Њ—А–Њ–љ–∞ \(CC1\) –≤—Ц–і–Њ–Љ–∞, –љ–µ–Њ–±—Е—Ц–і–љ–Њ –Ј–љ–∞–є—В–Є \(CM\). –†–Њ–Ј–≥–ї—П–љ–µ–Љ–Њ –Њ—Б–љ–Њ—Б—Г –њ—А–Є–Ј–Љ–Є - —А—Ц–≤–љ–Њ–±—Ц—З–љ—Г —В—А–∞–њ–µ—Ж—Ц—О \(ABCD\). –Ч–∞ —Г–Љ–Њ–≤–Њ—О –Ј–∞–≤–і–∞–љ–љ—П \(CM || AB\) —Ц –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ \(AB = CM\) (—П–Ї —Б—В–Њ—А–Њ–љ–Є –њ–∞—А–∞–ї–µ–ї–Њ–≥—А–∞–Љ–∞). –Ч–љ–∞–є–і–µ–Љ–Њ \(CM\). –Ю–±вАЩ—Ф–Љ –њ—А–Є–Ј–Љ–Є –і–Њ—А—Ц–≤–љ—О—Ф 672 \(—Б–Љ ^ 3 \) \(V_ {–њ—А} = S_ {–Њ—Б–љ} * h_ {–њ—А}\), –і–µ \(h_ {–њ—А} = CC1 = 8 —Б–Љ\). –Ю—Б–љ–Њ–≤–Њ—О —Ф —В—А–∞–њ–µ—Ж—Ц—П, –њ–ї–Њ—Й–∞ —В—А–∞–њ–µ—Ж—Ц—Ч –і–Њ—А—Ц–≤–љ—О—Ф \(S_ {—В—А} = \frac {a + b}{2} * h_ {—В—А} \), –і–µ \(a \) —Ц \(b \) - –Њ—Б–љ–Њ–≤–Є —В—А–∞–њ–µ—Ж—Ц—Ч (AD, BC), \(AD = 6 * BC = 6 * CP = 6x\) (–њ–Њ–Ј–љ–∞—З–Є–Љ–Њ –Ј–∞ x = –Т–°). $$V_{–њ—А} = S_{–Њ—Б–љ}*h_{–њ—А} => V_{–њ—А} = \frac{AD + BC}{2}*h_{—В—А}*h_{–њ—А} => \\ V_{–њ—А } = \frac{6x + x}{2}*6x*8 => 672 = \frac{42x^2}{2}*8 =>x^2 = 4 => x = 2 $$
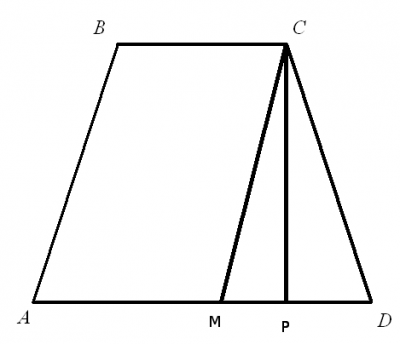
–†–Њ–Ј–≥–ї—П–љ–µ–Љ–Њ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є \( ќФ MCP, CP = h_ {—В—А} = 6 * x\) –љ–∞ –њ—Ц–і—Б—В–∞–≤—Ц —В–µ–Њ—А–µ–Љ–Є –Я—Ц—Д–∞–≥–Њ—А–∞ –Њ–і–µ—А–ґ–Є–Љ–Њ \(MC = \sqrt{MP^2 + CP^2}\). –Ч —Г–Љ–Њ–≤–Є –Ј–∞–≤–і–∞–љ–љ—П –≤—Ц–і–Њ–Љ–Њ , —Й–Њ \(CP = AD = 6 * BC = 6x = 12\), \(AB | | MC => ABCM\) - –њ–∞—А–∞–ї–µ–ї–Њ–≥—А–∞–Љ => \(AB = MC = CD => ќФMCD\) - —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї, –Ј–≥—Ц–і–љ–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ - –≤—Ц—Б–Њ—В–∞, –±–µ—Б—Ц–Ї—В—А—Ц—Б–∞ —Ц –Љ–µ–і—Ц–∞–љ–∞, –Њ–њ—Г—Й–µ–љ—Ц –Ј –≤–µ—А—И–Є–љ–Є —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ –љ–∞ –є–Њ–≥–Њ –њ—Ц–і—Б—В–∞–≤—Г —А—Ц–≤–љ—Ц —Ц –Ј–±—Ц–≥–∞—О—В—М—Б—П –Њ—В—А–Є–Љ–∞—Ф–Љ–Њ $$MP = PD = \frac{1}{2} MD = \frac{AD-BC}{2} = \frac{6*x-x}{2} = \frac{5*x}{2} = \frac{5*2}{2} = 5,\\ MC = \sqrt{MP^2 + CP^2} = \sqrt{5^2 + 12^2} = \sqrt{169} = 13\\S_{CC_{1}M_{1}M}=MC*CC_1 =13 * 8 = 104 $$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 104 \(—Б–Љ^2\)

