–Ч–Љ—Ц—Б—В –Ј–∞–≤–і–∞–љ–љ—П: –Ю–±—З–Є—Б–ї—Ц—В—М \( \frac{1}{\pi}\int_{-5}^{0} \sqrt{25-x^2}dx \), –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—З–Є —А—Ц–≤–љ—П–љ–љ—П –Ї–Њ–ї–∞ \(x^2+y^2=25\), –Ј–Њ–±—А–∞–ґ–µ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї—Г.
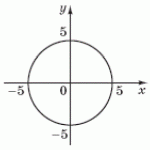
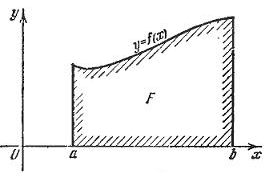
–Ґ–µ–Њ—А—Ц—П –і–Њ –Ј–∞–≤–і–∞–љ–љ—П: –У–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—В –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞. –ѓ–Ї—Й–Њ \(f (x)\) –љ–µ–њ–µ—А–µ—А–≤–љ–∞ —Ц –њ–Њ–Ј–Є—В–Є–≤–љ–∞ –љ–∞ –≤—Ц–і—А—Ц–Ј–Ї—Г [a, b], —В–Њ —Ц–љ—В–µ–≥—А–∞–ї —Ф –њ–ї–Њ—Й–∞ –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч, –Њ–±–Љ–µ–ґ–µ–љ–Њ—Ч –ї—Ц–љ—Ц—П–Љ–Є \(y = 0, x = a, x = b, y = f (x) \)
–†—Ц—И–µ–љ–љ—П: –Ч–≥—Ц–і–љ–Њ –Ј "–Ґ–µ–Њ—А—Ц—Ф—О –і–Њ –Ј–∞–≤–і–∞–љ–љ—П" –Љ–Њ–ґ–љ–∞ –Ј—А–Њ–±–Є—В–Є –≤–Є—Б–љ–Њ–≤–Њ–Ї, —Й–Њ –≤ –Ј–∞–≤–і–∞–љ–љ—Ц –њ–Њ—В—А—Ц–±–љ–Њ –Ј–љ–∞–є—В–Є –њ–ї–Њ—Й—Г —Д—Ц–≥—Г—А–Є –љ–∞ –≤—Ц–і—А—Ц–Ј–Ї—Г [-5, 0], –Њ–±–Љ–µ–ґ–µ–љ—Г –Ј–≤–µ—А—Е—Г –Ї—А–Є–≤–Њ—О –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—Ц, –Ј–љ–Є–Ј—Г –≤—Ц—Б—Б—О \(x \), –њ—А–∞–≤–Њ—А—Г—З –≤—Ц—Б—Б—О \(y \), –ї—Ц–≤–Њ—А—Г—З –≤–Њ–љ–∞ –њ–µ—А–µ—В–Є–љ–∞—Ф—В—М—Б—П –Ј –≤—Ц—Б—Б—О \(x \) - —Ж–µ –±—Г–і–µ —З–µ—А–≤–µ—А—В—М –Ї–Њ–ї–∞
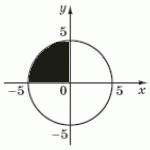
–£ –Ј–∞–і—Ц–љ—Ц—Ц –і–∞–љ–Њ —А—Ц–≤–љ—П–љ–љ—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—Ц \(x ^ 2 + y ^ 2 = 25 \), –і–µ \(r ^ 2 = 25 => r = 5 \). –ѓ–Ї –≤—Ц–і–Њ–Љ–Њ –њ–ї–Њ—Й–∞ –Ї–Њ–ї–∞ —А–Њ–Ј—А–∞—Е–Њ–≤—Г—Ф—В—М—Б—П –Ј–∞ —Д–Њ—А–Љ—Г–ї–Њ—О \(S = \pi r ^ 2 \). –Я–ї–Њ—Й–∞ —З–≤–µ—А—В—Ц –Ї–Њ–ї–∞ –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ \(\frac{s}{4} \). –Я—Ц–і—Б—В–∞–≤–Є–Љ–Њ –Њ—В—А–Є–Љ–∞–љ—Ц –Ј–∞—З–µ–љ–Є–µ –≤ —Д–Њ—А–Љ—Г–ї—Г \(S_ {\frac {1}{4}} = \int_{-5}^{0} \sqrt{25-x^2}dx = \frac {1}{4} \pi r ^ 2 \).$$ \frac{1}{\pi}\int_{-5}^{0} \sqrt{25-x^2}dx = \frac{1}{\pi} (\frac {1}{4} \pi r ^ 2) = \frac {1}{4} 5^2 = 6.25$$–Т—Ц–і–њ–Њ–≤—Ц–і—М: 6.25.

