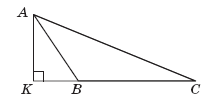
Зміст завдання : У трикутнику ABC основа висоти AK лежить на продовженні сторони BC (див. рисунок). AK =6 см, KB = \(2\sqrt 3\). Радіус описаного навколо трикутника ABC кола дорівнює \(15\sqrt 3\). Визначте довжину AC.
Теорія до завдання:
Теорема синусів - теорема, що встановлює залежність між сторонами довільного трикутника та противолежащими їм кутами. Теорема стверджує, що сторони трикутника пропорційні синусам протилежних кутів, або, у розширеній формулюванні:$$ \frac {a}{\sin \alpha} = \frac{b}{\ sin \beta} = \frac{c}{\ sin \gamma} = 2R $$де \(a,b,c\), - сторони трикутника, \(\alpha, \beta, \gamma \)- відповідно протилежні їм кути, а \(R\)- радіус кола, описаного навколо трикутника.
Рішення: Розглянемо \(\bigtriangleup\) ABC, згідно теореми синусів («Теорія до завдання»), \( \frac {AC} {\ sin \ ABC} = 2R \). З умови завдання випливає, що кути ABK і ABC є додатковими, тобто їх сума дорівнює \(180^0 => \ sin ABK = \ sin ABC \). Знайдемо \(\ sin ABK\) із \(\bigtriangleup\) AKB \(\ sin ABK= \frac{AK}{AB}\) . \(AB\) - діагональ прямокутного \(\bigtriangleup\) AKB і по теоремі Піфагора дорівнює \(\sqrt{AK^2 + KB^2}\). Підставив отримані значення у формулу $$\frac {AC} {\ sin \ ABK} = 2R => AC =2R *\sin \ ABK => AC =2R *\frac{AK}{AB} =>\\ AC =2R *\frac{AK}{\sqrt{AK^2 + KB^2}} => AC = 2*15\sqrt{3}\frac{6}{\sqrt{6^2 + (2\sqrt{3})^2}} =>\\ AC = 2*15\sqrt{3}\frac{6}{\sqrt{36 +12}} => AC = 2*15\sqrt{3}\frac{6}{4\sqrt{3}}=\frac{2*15*6}{4}= 45$$Відповідь: 45 см.

