Зовнішнє незалежне оцінювання 2012 року з математики (1 сесія). Завдання № 18.

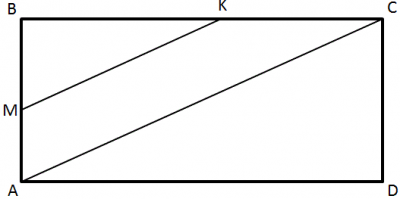
Зміст завдання : У прямокутнику ABCD: BC = 80, AC = 100. Через точки M і K, що належать сторонам AB і BC відповідно, проведено пряму, паралельну AC. Знайдіть довжину більшої сторони трикутника MBK, якщо BK = 20.

Теорія до завдання:
Ознаки подібності трикутників

1. За двома кутами: Якщо два кути одного трикутника рівні двом кутам іншого трикутника, то такі трикутники подібні.
2. За двома сторонами і кутом між ними: Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника й кути, утворені цими сторонами, рівні, то такі трикутники подібні.
3. За трьома сторонами: Якщо три сторони одного трикутника пропорційні трьом сторонам іншого трикутника, то такі трикутники подібні.

Рішення: з умови завдання відомо, що AC||MK, ∟BMK і ∟BAC - відповідні, як відомо відповідні кути рівні, тобто  ∟BMK = ∟BAC, аналогічно ∟BKM = ∟BCA.

ΔABC і ΔMBK подібні за першою ознакою. Запишемо пропорцію для відповідних сторін трикутників
$$\frac{BK}{BC}=\frac{MK}{AC}$$
З умови завдання відомо що AC = 100, BK = 20, BC = 80
$$\frac{20}{80}=\frac{MK}{100}$$$$MK=\frac{20*100}{80}=25$$
Відповідь: Г - 25.