Зовнішнє незалежне оцінювання 2012 року з математики (1 сесія). Завдання № 17.

Продовжуємо вивчати завдання зно з математики 2012

Теорія до завдання: Розвяжіть нерівність
$$(\frac{\pi}{4})^{x} <( \frac{4}{\pi} )^{3}$$

Відповіді до завдання:

Теорія до завдання: За визначенням степеня вважають, що якщо n - натуральне число, то
$$a^{-n}=\frac{1}{a^{n}}$$
Рішення: наведемо нерівність до загальної основи, для цього скористаємося формулою з розділу "Теорія до завдання" $$(\frac{4}{\pi})^{3} = (\frac{\pi}{4})^{-3}$$ підставимо в нерівність $$(\frac{\pi}{4})^{x} < (\frac{\pi}{4})^{-3}$$ основа ступеня \(\pi/4<1\) функція спадна , тобто більшому х відповідає менший у, отримаємо$$ x >-3$$

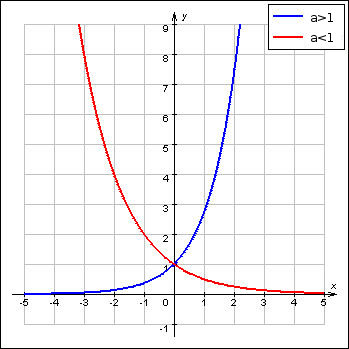
 графік степеневої функції \(y=a^x\)

Відповідь:  A: (-3; +∞) .