Зміст завдання : На рисунку зображено паралелограм ABCD, площа якого дорівнює 60 \(см^2\) . Точка М належить стороні BC. Визначте площу фігури, що складається з двох зафарбованих трикутників.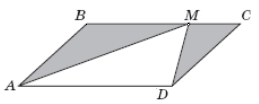
Відповіді до завдання:
А |
Б |
В |
Г |
Д |
\(45 см^2\) |
\(40 см^2\) |
\(35 см^2\) |
\(30 см^2\) |
\(20 см^2\) |
Теорія до завдання:
Паралелограм — це чотирикутник, у чкого протележні сторони паралельні.
Площа паралелограма обчислюєтся за формулою $$S_{пар} = a*h$$
h — висота,
a — сторона, до якої проведена ця висота.
Рішення: Площа зафарбованої фігури можна знайти двома способами
1. спосіб.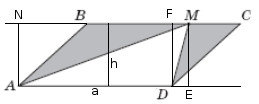
Площа шуканої фігури \(S_{фар} = S_{пар} (площі паралелограмма) - S_{тр} (площа трикутника AMD, не зафарбований)\).
Площа треугольнака дорівнює
$$S_{тр} = \frac{1}{2}* a * h$$
h - висота трикутника (ME).
a - сторона, до якої проведена ця висота (AD).
h паралелограмма і трикутника співпадають (ME = h)
Таким чином площа трикутника $$Sтр = \frac{1}{2} S_{пар}$$
$$S_{фар} = S_{пар} - S_{тр} = S_{пар} - \frac{1}{2} S_{пар} = \frac{1}{2} S_{пар} = \frac{1}{2} * 60 = 30 см^2$$
2. спосіб
Площа двох зафарбованих трикутників дорівнює сумі площ трикутників ABM і MCD.
$$S_{ABM}= \frac{1}{2} BM*AN = \frac{1}{2}(BC-MC)*h$$$$S_{MCD}=\frac{1}{2} MC*AN = {1}{2} MC*h$$$$S_{фар} = S_{ABM} + S_{MCD} = \frac{1}{2} (BC-MC)*h + \frac{1}{2} MC*h =$$$$= \frac{1}{2} h ( BC-MC+ MC) = \frac{1}{2} h*BC = \frac{1}{2} h*a =\frac{1}{2}60 = 30 см^2$$
Відповідь: Г: 30 \(см^2\).

