Зміст завдання : Висота правильної чотирикутної піраміди дорівнює 4 см, а її апофема — 5 см. Визначте косинус кута між площиною бічної грані піраміди і площиною основи.
А |
Б |
В |
Г |
Д |
\(\frac{1}{5}\) |
\(\frac{3}{5}\) |
\(\frac{3}{4}\) |
\(\frac{4}{5}\) |
\(\frac{4}{3}\) |
Теорія до завдання: Піраміда називається правільною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника.
Віссю правильної піраміди є пряма, що містить її висоту.
Апофемою є проведена з вершини висота бічної грані правильної піраміди.
Правильна чотирикутна піраміда
В основі правильної чотирикутної піраміди лежить квадрат, який зображується довільним паралелограмом. Його центром є точка перетину діагоналей. Ця точка — основа висоти піраміди.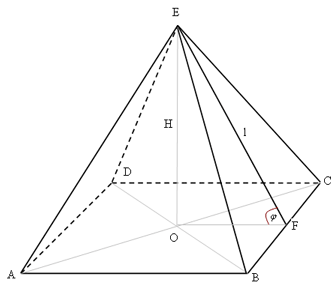
O -основа висоти піраміди (H).
l (EF)- Апофема піраміди.
Рішення: Для того щоб визначити косинус кута між площиною бічної грані піраміди і площиною основи потрібно постотроіть цей кут. Нам необхідно взяти деяку точку на прямій перетину бічної грані піраміди і площиною основи (CB)(див. рисунок). Через цю точку (F) провести перпендикуляри до прямої в кожній із площин. Кут між цими перпендикулярами буде кутом між даними площинами.
Згідно умови завдання перпендикуляр бічній грані відомий - апофема. Так як бічна грань - рівнобедрений трикутник, то апофема (висота рівнобедреного трикутника) збігається з медіаною, тобто F - середина CB. Перпендикуляр в точці F в площі основи - середня лінія, яка проходить через точку О - центр чотирикутника. Розглянемо трикутник EOF. Це прямокутний трикутник в якому відома EO - висота правільної чотірікутної піраміди, яка дорівнює 4 см і EF - апофема - 5 см.$$\cos\phi = \frac{OF}{EF}$$Знайдемо OF з трикутника EOF по теоремі Піфагора $$OF_{2} = EF_{2} - EO_{2}$$$$OF_{2} = 52 - 42 = 25 - 16 = 9$$$$OF = 3$$$$\cos\phi = \frac{OF}{EF} = \frac{3}{5}$$
Відповідь: Б: \(\frac{3}{5}\).

