–Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б—А–∞–≤–љ–Є—В—М –і–≤–∞ –ї–Њ–≥–∞—А–Є—Д–Љ–∞, –љ–∞–њ—А–Є–Љ–µ—А \(log_{4}{5}\) –Є \(\log_{5}{6}\). –Ф–ї—П —А–µ—И–µ–љ–Є—П –±—Г–і–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–µ —Б–њ–Њ—Б–Њ–±—Л:
–Я–µ—А–≤—Л–є —Б–њ–Њ—Б–Њ–±¬†(–≤—Л—З–Є—В–∞–љ–Є–µ –µ–і–Є–љ–Є—Ж—Л).
–Ш–Ј –Ї–∞–ґ–і–Њ–≥–Њ –ї–∞–≥–Њ—А–Є—Д–Љ–∞ –≤—Л—З—В–µ–Љ –њ–Њ 1.$$ log_{4}{5} - 1 = log_{4}{\frac{5}{4}}$$$$ log_{5}{6} - 1 = log_{5}{\frac{6}{5}}$$
–Т–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ —Б–≤–Њ–є—Б—В–≤–Њ–Љ –ї–∞–≥–Њ—А–Є—Д–Љ–Є
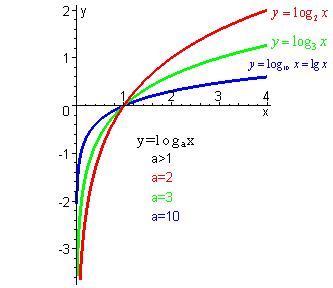
–µ—Б–ї–Є c > a > 1, —В–Њ –њ—А–Є b > 1 —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ –љ–µ—А–∞–≤–µ–љ—Б—В–≤–Њ \(log_{a}{b} > log_{c}{b}\). –У—А–∞—Д–Є—З–µ—Б–Ї–Є —Н—В–Њ —Е–Њ—А–Њ—И–Њ –≤–Є–і–љ–Њ, –Ї—А–∞–≤–∞—П –ї–Њ–≥–∞—А–Є—Д–Љ–∞ —Б –±–Њ–ї—М—И–Є–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ –ї–µ–ґ–Є—В –љ–Є–ґ–µ –Ї—А–Є–≤–Њ–є –ї–Њ–≥–∞—А–Є—Д–Љ–∞ —Б –Љ–µ–љ—М—И–Є–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ $$ log_{5}{\frac{6}{5}} < log_{4}{\frac{6}{5}}$$
–Ф–∞–љ–љ—Л–є –њ—А–Є–µ–Љ –±—Л–ї —Б–і–µ–ї–∞–љ, —З—В–Њ–±—Л –њ–µ—А–µ–є—В–Є –Ї –Њ—Б–љ–Њ–≤–∞–љ–Є—О 4. –≠—В–Њ –і–∞—Б—В –љ–∞–Љ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –њ—А–Њ–≤–µ—Б—В–Є —Б—А–∞–≤–љ–µ–љ–Є–µ —Б–Њ –≤—В–Њ—А—Л–Љ –ї–Њ–≥–∞—А–Є—Д–Љ–Њ–Љ$$ log_{5}{\frac{6}{5}} < log_{4}{\frac{6}{5}} < log_{4}{\frac{5}{4}}$$ –Т—В–Њ—А–Њ–µ –љ–µ—А–∞–≤–µ–љ—Б—В–≤–Њ –±—Л–ї–Њ –њ–Њ–ї—Г—З–µ–љ–Њ –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є —Б–≤–Њ–є—Б—В–≤–∞ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ—Б—В–Є –ї–Њ–≥–∞—А–Є—Д–Љ–∞, —В.–Ї. –Њ—Б–љ–Њ–≤–∞–љ–Є–µ –ї–Њ–≥–∞—А–Є—Д–Љ–∞ >1, –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В, —В.–µ –±–Њ–ї—М—И–µ–Љ—Г –Ј–љ–∞—З–µ–љ–Є—О —З–Є—Б–ї–∞ –њ–Њ–і –ї–∞–≥–Њ—А–Є—Д–Љ–Њ–Љ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –±–Њ–ї—М—И–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –ї–Њ–≥–∞—А–Є—Д–Љ–∞.¬† \(\frac{6}{5} < \frac{5}{4}\) —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ–Њ–ї—Г—З–Є–ї–Є $$log_{5}{\frac{6}{5}} < log_{4}{\frac{5}{4}}$$$$log_{5}{\frac{6}{5}}+1 < log_{4}{\frac{5}{4}}+1$$$$log_{5}{6} < log_{4}{5}$$
–Т—В–Њ—А–Њ–є —Б–њ–Њ—Б–Њ–±¬†(–љ–µ—А–∞–≤–µ–љ—Б—В–≤–Њ –Ъ–Њ—И–Є).
–Ч–∞–њ–Є—И–µ–Љ –љ–µ—А–∞–≤–µ–љ—Б—В–≤–Њ $$\sqrt{ab}< \frac{a+b}{2}$$ –≥–і–µ a>0, b>0. –Т –љ–∞—И–µ–Љ —Б–ї—Г—З–∞–µ –љ–µ—А–∞–≤–µ–љ—Б—В–≤–Њ –Љ–Њ–ґ–љ–Њ –њ—А–Є–Љ–µ–љ–Є—В—М,—В.–Ї. —З–Є—Б–ї–∞ –њ–Њ–і –ї–∞–≥–Њ—А–Є—Д–Љ–Њ–Љ >1. —В.–µ. –ї–Њ–≥–∞—А–Є—Д–Љ—Л –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ—Л–µ. –Т –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є –Љ—Л –≤–Є–і–µ–Љ —Б–ї–Њ–ґ–µ–љ–Є–µ a+b , —В.–µ. –њ—А–Є–і–µ—В—Б—П —Б–Ї–ї–∞–і—Л–≤–∞—В—М –і–≤–∞ –ї–Њ–≥–∞—А–Є—Д–Љ–∞, –њ–Њ—Н—В–Њ–Љ—Г –Њ–±–Њ–Ј–љ–∞—З–Є–Љ –Ј–∞ –∞ = \(log_{5}{4}=\frac{1}{\log_{4}{5}}\), b = \(log_{5}{6}\)
–Я–Њ–і—Б—В–∞–≤–Є–ї –ї–Њ–≥–∞—А–Є—Д–Љ—Л –≤ —Д–Њ—А–Љ—Г–ї—Г $$\sqrt{\log_{5}{4} \log_{5}{6}}< \frac{\log_{5}{4}+ \log_{5}{6}}{2} \Rightarrow$$$$\sqrt{\frac{\log_{5}{6}}{\log_{4}{5}}}< \frac{\log_{5}{4}+ \log_{5}{6}}{2} \Rightarrow$$$$\sqrt{\frac{\log_{5}{6}}{\log_{4}{5}}}< \frac{\log_{5}{24}}{2} < \frac{\log_{5}{25}}{2} \Rightarrow$$$$\sqrt{\frac{\log_{5}{6}}{\log_{4}{5}}}< \frac{\log_{5}{24}}{2} < 1\Rightarrow$$$$\sqrt{\frac{\log_{5}{6}}{\log_{4}{5}}} < 1$$–≤–Њ–Ј–≤–µ–і–µ–Љ –≤ –Ї–≤–∞–і—А–∞—В –Њ–±–µ —З–∞—Б—В–Є –љ–µ—А–∞–≤–µ–љ—Б—В–≤–∞$$\frac{\log_{5}{6}}{\log_{4}{5}} < 1\Rightarrow$$$$\log_{5}{6}<\log_{4}{5}$$

