–Ч–Љ—Ц—Б—В –Ј–∞–≤–і–∞–љ–љ—П : –ѓ–Ї–Њ–Љ—Г –њ—А–Њ–Љ—Ц–ґ–Ї—Г –љ–∞–ї–µ–ґ–Є—В—М –Ј–љ–∞—З–µ–љ–љ—П –≤–Є—А–∞–Ј—Г \(\sin 410^0\)?
–Т—Ц–і–њ–Њ–≤—Ц–і—Ц –і–Њ –Ј–∞–≤–і–∞–љ–љ—П:
 
–Р |
–С |
–Т |
–У |
–Ф |
(-1;-\(\frac{1}{2}\)) |
(-\(\frac{1}{2}\);\(\frac{1}{2}\)) |
(\(\frac{1}{2}\);\(\frac{\sqrt{2}}{2}\)) |
(\(\frac{\sqrt{2}}{2}\);\(\frac{\sqrt{3}}{2}\)) |
(\(\frac{\sqrt{3}}{2}\);1) |
–Ґ–µ–Њ—А—Ц—П –і–Њ –Ј–∞–≤–і–∞–љ–љ—П: –¶–µ –Ј–∞–≤–і–∞–љ–љ—П –љ–∞ –Ј–љ–∞–љ–љ—П –љ–∞—Б—В—Г–њ–љ–Њ–≥–Њ:
- —Д—Г–љ–Ї—Ж—Ц—П \(\sin\) - –њ–µ—А—Ц–Њ–і–Є—З–љ–∞ —Д—Г–љ–Ї—Ж—Ц—П –Ј –њ–µ—А—Ц–Њ–і–Њ–Љ \(360^0 (2\pi)\).
- –љ–µ–Њ–±—Е—Ц–і–љ–Њ –Ј–љ–∞—В–Є –Ј–љ–∞—З–µ–љ–љ—П —В—А—Ц–≥–Њ–љ–њ–Љ–µ—В—А—Ц—З–µ—Б–Ї—Ц–є —Д—Г–љ–Ї—Ж—Ц—П –і–µ—П–Ї–Є—Е –Ї—Г—В—Ц–≤
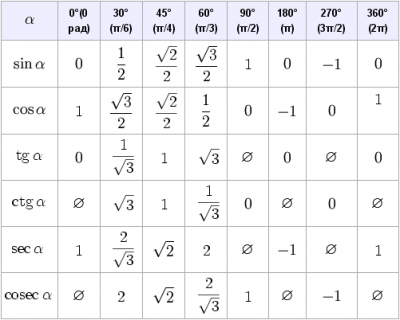
–†—Ц—И–µ–љ–љ—П: \(\sin 410^0\) ,—В.–Ї —Д—Г–љ–Ї—Ж—Ц—П sin –њ–µ—А—Ц–Њ–і–Є—З–љ–∞ —Д—Г–љ–Ї—Ж—Ц—П –Ј –њ–µ—А—Ц–Њ–і–Њ–Љ \(360^0\), —В–Њ \(\sin 410^0 = \sin (410^0 - 360^0) = \sin 50^0\)
–Ф–Є–≤–Є–Љ–Њ—Б—П –≤ —А–Њ–Ј–і—Ц–ї "–Ґ–µ–Њ—А—Ц—П –і–Њ –Ј–∞–≤–і–∞–љ–љ—П" —Ц –±–∞—З–Є–Љ–Њ, —Й–Њ $$\sin45^0 < \sin 50^0 < \sin60^0$$$$\frac{\sqrt{2}}{2} < \sin 50^0 < \frac{\sqrt{3}}{2}$$–Ф–Є–≤–Є–Љ–Њ—Б—П –љ–∞ –њ—А–Њ–њ–Њ–љ–Њ–≤–∞–љ—Ц –≤—Ц–і–њ–Њ–≤—Ц–і—Ц —Ц –њ—Ц–і–±–Є—А–∞—Ф–Љ–Њ —Ц–љ—В–µ—А–≤–∞–ї, —П–Ї—Ц –њ—Ц–і—Е–Њ–і–Є—В—М.
–Т—Ц–і–њ–Њ–≤—Ц–і—М: –У: (\(\frac{\sqrt{2}}{2}\);\(\frac{\sqrt{3}}{2}\)).

