–Ч–∞–≤–і–∞–љ–љ—П:¬†–Т—Ц–і—А—Ц–Ј–Њ–Ї AB –њ–µ—А–µ—В–Є–љ–∞—Ф –њ–ї–Њ—Й–Є–љ—Г \(\alpha\) –≤ —В–Њ—З—Ж—Ц 0. –Я—А–Њ–µ–Ї—Ж—Ц—Ч –≤—Ц–і—А—Ц–Ј–Ї—Ц–≤ AO —Ц BO –љ–∞ —Ж—О –њ–ї–Њ—Й–Є–љ—Г –і–Њ—А—Ц–≤–љ—О—О—В—М 5 —Б–Љ —Ц 20 —Б–Љ –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ. –Ч–љ–∞–є–і—Ц—В—М –і–Њ–≤–ґ–Є–љ—Г –≤—Ц–і—А—Ц–Ј–Ї–∞ AB, —П–Ї—Й–Њ AO = 8—Б–Љ.
–Т–∞—А—Ц–∞–љ—В –≤—Ц–і–њ–Њ–≤—Ц–і—Ц:¬†$$\begin{array}{|c|c|c|c|c|} ¬† –Р &–С & –Т & –У & –Ф \\ \hline \\¬†10 —Б–Љ &¬†22 —Б–Љ¬†&¬†32 —Б–Љ & 40 —Б–Љ¬†&¬†52 —Б–Љ¬† \end{array}$$
–†—Ц—И–µ–љ–љ—П:¬†–њ–Њ—Б—В—А–Њ–Є–Љ —А–Є—Б—Г–љ–Њ–Ї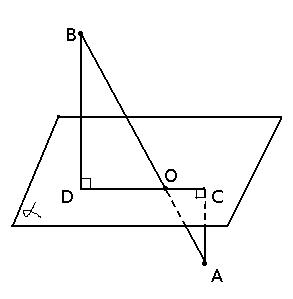 ¬†
 
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ–Њ—Б—В—А–Њ–Є—В—М —А–Є—Б—Г–љ–Њ–Ї, –Њ–њ—Г—Б—В–Є–Љ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А—Л –Є–Ј –Ї–Њ–љ—Ж–Њ–≤ –Њ—В—А–µ–Ј–Ї–∞ \(AB\) –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В—М. –Я—А—П–Љ—Л–µ \(BD||AC\) –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–µ, —В.–µ. —З–µ—А–µ–Ј –љ–Є—Е –Љ–Њ–ґ–љ–Њ –њ—А–Њ–≤–µ—Б—В–Є —В–Њ–ї—М–Ї–Њ –Њ–і–љ—Г –њ–ї–Њ—Б–Ї–Њ—Б—В—М. –≠—В–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В—М –±—Г–і–µ—В –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є \(\alpha\) –Є –≤ —Н—В–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –±—Г–і–µ—В –ї–µ–ґ–∞—В—М –Њ—В—А–µ–Ј–Њ–Ї \(AB\). –Т—Б–µ —Н—В–Є –њ–Њ—П—Б–љ–µ–љ–Є—П –љ—Г–ґ–љ—Л, —З—В–Њ–±—Л –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –і–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФACO\) –Є \(ќФBDO\) –ї–µ–ґ–∞—В –≤ –Њ–і–љ–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –Є –Њ–љ–Є —П–≤–ї—П—О—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–Љ–Є. –Ш–Ј —А–Є—Б—Г–љ–Ї–∞ –≤–Є–і–љ–Њ, —З—В–Њ –і–≤–∞ —Г–≥–ї–∞ \(\angle COA = \angle BOD \) - –Ї–∞–Ї –і–≤–∞ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л—Е —Г–≥–ї–∞ .¬†
–Ш–Ј —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є —Б–ї–µ–і—Г–µ—В, —З—В–Њ \(OC= 5–Љ—Б \), \(OD= 20–Љ—Б \)¬†, \(AO= 8–Љ—Б \).¬†
–Ш–Ј \(ќФACO\) —Б–ї–µ–і—Г–µ—В \(\cos(\angle COA) = \frac{OC}{AO} = \frac{5}{8}\)
–Ш–Ј \(ќФBDO\) —Б–ї–µ–і—Г–µ—В \(\cos(\angle BOD) = \frac{OD}{BO} = \frac{20}{BO}\)
 \(\cos(\angle COA) = \cos(\angle BOD) => \frac{5}{8} = \frac{20}{BO} => BO = \frac{20*8}{5} = 32\)
–Ф–ї–Є–љ–∞ –Њ—В—А–µ–Ј–Ї–∞ \(AB = AO + BO = 8 + 32 = 40—Б–Љ\)¬†
¬†–Т—Ц–і–њ–Њ–≤—Ц–і—М: \(–У\)
¬†¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 17¬† ¬† ¬†–љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 19
 

