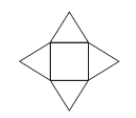
Завдання: На рисунку зображено розгортку піраміди, що складається з квадрата, сторона якого дорівнює 10 см, і чотирьох правильних трикутників. Визначте площу бучної поверхні цієї піраміди \(\text{у см}^2\)
Варіант відповіді: $$\begin{array}{|c|c|c|c|c|} А &Б & В & Г & Д \\ \hline \\ 100\sqrt{3} & 100 & 400\sqrt{3} &100(1+\sqrt{3}) & 200 \end{array}$$
Рішення: Площадь боковой поверхности пирамиды равно площади четырех правильных треугольников (квадрат - основание пирамиды). Площадь правильного треугольника равна $$S_{Δ} = \frac{\sqrt{3}}{4}a^2$$ Тогда, площадь боковой поверхности равна $$S_{б.пов.} = 4S_{Δ} = 4\frac{\sqrt{3}}{4}a^2 = \sqrt{3}a^2$$ подставляем в полученную формулу длину стороны \(a=10\) и получаем ответ $$a^2 \sqrt{3} = 100 \sqrt{3}$$
Відповідь: \(А\)
попереднє завдання № 15 наступне завдання № 17
