–Ч–∞–≤–і–∞–љ–љ—П: –Ю—Б–љ–Њ–≤–Њ—О –њ—Ц—А–∞–Љ—Ц–і–Є \(SABCD\) —Ф —В—А–∞–њ–µ—Ж—Ц—П \(ABCD\) \(BC||AD\). –С—Ц—З–љ–∞ –≥—А–∞–љ—М \(SBC\), –њ–ї–Њ—Й–∞ —П–Ї–Њ—Ч –і–Њ—А—Ц–≤–љ—О—Ф \(24,4—Б–Љ^2\), –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –і–Њ –њ–ї–Њ—Й–Є–љ–Є –Њ—Б–љ–Њ–≤–Є –њ—Ц—А–∞–Љ—Ц–і–Є. –Ґ–Њ—З–Ї–∞ \(M\) - —Б–µ—А–µ–і–Є–љ–∞ —А–µ–±—А–∞ \(SB\). –Я–ї–Њ—Й–Є–љ–∞ \(MAD\) –њ–µ—А–µ—В–Є–љ–∞—Ф —А–µ–±—А–Њ \(SC\) –≤ —В–Њ—З—Ж—Ц \(N\). –Т–Є–Ј–љ–∞—З—В–µ –і–Њ–≤–ґ–Є–љ—Г –≤—Ц–і—А—Ц–Ј–Ї–∞ \(MN\) (—Г —Б–Љ), —П–Ї—Й–Њ –Њ–±вАЩ—Ф–Љ –њ—Ц—А–∞–Љ—Ц–і–Є –і–Њ—А—Ц–≤–љ—О—Ф \(152 —Б–Љ^3\), –∞ –њ–ї–Њ—Й–∞ —Ч—Ч –Њ—Б–љ–Њ–≤–Є - \(57 —Б–Љ^2\).
–†—Ц—И–µ–љ–љ—П:¬†
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–Є—Б—Г–љ–Њ–Ї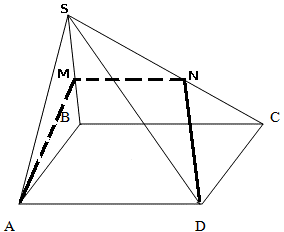
–Ф–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ \(MN\) - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФSBC\).
–°—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞¬† - –Њ—В—А–µ–Ј–Њ–Ї, —Б–Њ–µ–і–Є–љ—П—О—Й–Є–є —Б–µ—А–µ–і–Є–љ—Л –і–≤—Г—Е –µ–≥–Њ —Б—В–Њ—А–Њ–љ. –°—А–µ–і–љ—П—П –ї–Є–љ–Є—П –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ —В—А–µ—В–µ–є —Б—В–Њ—А–Њ–љ–µ –Є —А–∞–≤–љ–∞ –µ–µ –њ–Њ–ї–Њ–≤–Є–љ–µ.
–Ґ–Њ—З–Ї–∞ M - —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л \(BS\)¬† –њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є, –Њ—Б—В–∞–ї–Њ—Б—М –і–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ–±—Л \(MN\) –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ \(BC\) \(MN||BC\).
–Ф–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ: –њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є \(AD||BC\) –Ї–∞–Ї —Б—В–Њ—А–Њ–љ—Л —В—А–∞–њ–µ—Ж–Є–Є. –Я–ї–Њ—Б–Ї–Њ—Б—В—М¬† \(MADN\) –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б—В–Њ—А–Њ–љ—Г \(AD\) —В—А–∞–њ–µ—Ж–Є–Є, —В–Њ–≥–і–∞ —Б–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–µ–Љ—Л, –µ—Б–ї–Є –њ—А—П–Љ–∞—П, –Ї–Њ—В–Њ—А–∞—П –љ–µ –њ—А–Є–љ–∞–і–ї–µ–ґ–Є—В –њ–ї–Њ—Б–Ї–Њ—Б—В–Є, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ –Ї–∞–Ї–Њ–є-–ї–Є–±–Њ –њ—А—П–Љ–Њ–є –≤ —Н—В–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є, —В–Њ —Н—В–∞ –њ—А—П–Љ–∞—П –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є, –Њ—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —Б—В–Њ—А–Њ–љ–∞ —В—А–∞–њ–µ—Ж–Є–Є \(BC\) –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є \(MADN\). –Я—А—П–Љ–∞—П \(MN\) - –њ–µ—А–µ—Б–µ—З–µ–љ–Є–µ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є \(MADN\) –Є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –љ–∞ –Ї–Њ—В–Њ—А–Њ–є –ї–µ–ґ–Є—В –≥—А–∞–љ—М \(SBC\), —В.–Ї. \(BC\) –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є \(MADN\), —В–Њ –Њ–љ–∞ –±—Г–і–µ—В –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ –њ—А—П–Љ–Њ–є \(MN\), —В.–µ. –Њ—В—А–µ–Ј–Ї–Є \(MN||BC\) –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л,—В.–µ \(MN\) - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФSBC\) –Є¬† \(MN = \frac{1}{2}BC\).
–Э–∞–є–і–µ–Љ —Б—В–Њ—А–Њ–љ—Г \(BC\). –≠–ї—П —Н—В–Њ–≥–Њ –≤ —Г—Б–ї–Њ–≤–Є–Є –і–∞–љ–∞ –њ–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФSBC\), –Ї–Њ—В–Њ—А–∞—П —А–∞–≤–љ–∞ $$S_{ќФSBC} = \frac{1}{2}SB*BC = 24.4 => BC = \frac{48.8}{SB} \quad (1)$$ \(SB = H\)¬† - –≤—Л—Б–Њ—В–∞ —В—А–∞–њ–µ—Ж–Є–Є, –∞ –≤ —В—А–∞–њ–µ—Ж–Є–Є –Є–Ј–≤–µ—Б—В–µ–љ –µ–µ –Њ–±—К–µ–Љ $$V = \frac{1}{3}S_{–Њ—Б–љ}H$$ –≥–і–µ –њ–Њ —Г—Б–ї–Њ–≤–Є—О \(S_{–Њ—Б–љ} = 57—Б–Љ^2\), –њ–Њ–ї—Г—З–∞–µ–Љ $$\frac{1}{3}57*H = 152 => H = 8$$ –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ —А–µ–Ј—Г–ї—М—В–∞—В –≤ (1) $$BC = \frac{48.8}{H}¬† = \frac{48.8}{8} = 6.1$$ –Ь—Л —Г–ґ–µ –њ–Њ–ї—Г—З–Є–ї–Є, —З—В–Њ —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П $$MN = \frac{1}{2}BC => NB = 3.05$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: $$\begin{array}{|c|c|c|}\hline & &¬† & 3& , &0 &5 & \\ \hline \hline \end{array} $$
¬† –њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 32 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 34

