Завдання: На рисунку схематично зображено опуклий міст, що має форму дуги \(AMB\) кола з центром у точці \(O\). \(MN\) - серединний перпендикуляр до \(AB\), \(MN = 3м\). Визначте довжину радіуса \(OB\) (у м), якщо довжина відрізка \(AB\) дорівнює 12 м..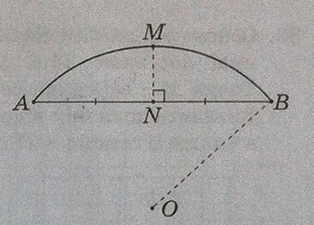
Рішення:
Опустим перпендяр из центра окружности на хорду \(AB\). Этот перпендикуляр пройдет через т. \(N\). Рассмотрим треугольник \(ΔONB\) - это прямоугольный треугольник. По теореме Пифагора получим $$OB^2 = ON^2 + NB^2 \quad (1)$$ Из условия задачи
\(NB = \frac{1}{2}AB = \frac{1}{2}12 = 6\),
обозначим \(R\) - радиус окружности, тогда \(OB = R\), \(OM = R = ON + NM => ON = R - MN = R - 3\). Подставляем в (1)
$$R^2 = (R - 3)^2 + 6^2 => R^2 = R^2 - 6R + 9 + 36 => R = 7.5$$
Відповідь: $$\begin{array}{|c|c|c|}\hline & & & 7& , &5 & & \\ \hline \hline \end{array} $$
Пробне ЗНО 2014 року з математики . Завдання № 31.
Темы:
математика, зно, пробне зно з математики, пробне зно 2014, ,

