Зміст завдання : Визначте, у скільки разів збільшується об’єм повітряної бульбашки, яка спливає з глибини 15 м до поверхні озера. Вважайте, що температура рідин та газів стала, атмосферний тиск дорівнює \(100 кПа\), \( g = 10 м/с^2\), густина води становить \(1000 кг/м^3\). Поверхневим натягом знехтуйте.
Відповіді до завдання:
А |
Б |
В |
Г |
у 2,5 раза
|
у 2 рази |
у 1,5 раза |
у 5 разів |
Теорія до завдання: Закон Бойля-Маріота (Ізотермічний процес).
Ізотермі́чний проце́с — фізичний процес, під час якого температура не змінюється. Ізотермічний процес відбувається достатньо повільно для того, щоб температура підтримувалася сталою завдяки теплообміну із середовищем. При ізотермічному стисненні тіло віддає тепло в середовище, при ізотермічному розширенні — вбирає тепло із середовища.
$$ p_{1}V_{1} = p_{2}V_{2} $$
Рішення:
із закону Бойля-Маріота отримаємо \(\frac{V_{2}}{V_{1}} = \frac{p_{1}}{p_{2}} \) таким чином, щоб відповісти на питання у скільки разів збільшиться об'єм кулі необхідно знайти відношення тисків на кулю на глибині 15м і на поверхні. На глибині 15м на кулю діє тиск рідини і атмосферний тиск, а на поверхні тільки атмосферний тиск.
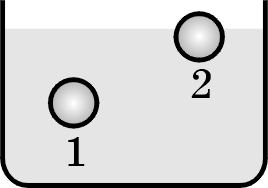$$ \frac{V_{2}}{V_{1}} = \frac{p_{1}}{p_{2}} \Rightarrow $$$$ \frac{V_{2}}{V_{1}} = \frac{p_{жид}+p_{атм}}{p_{атм}} \Rightarrow $$
$$ \frac{V_{2}}{V_{1}} = 1+\frac{p_{жид}}{p_{атм}} \Rightarrow $$$$ \frac{V_{2}}{V_{1}} = 1+\frac{\rho gh}{p_{атм}} \Rightarrow $$
підставимо значення $$ \frac{V_{2}}{V_{1}} = 1+\frac{1000 кг/м^3 * 10 м/с * 15 м}{100 кПа} \Rightarrow $$$$ \frac{V_{2}}{V_{1}} = 1+\frac{3}{2} \Rightarrow $$$$ \frac{V_{2}}{V_{1}} = 2,5 $$
Відповідь: А: у 2,5 раза
.
