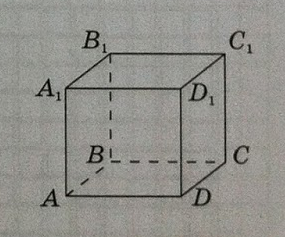
Завдання: На рисунку зображено куб \(ABCDA_1B_1C_1D_1\), ребро якого дорівнює \(1 \text{ см}\). Обчисліть відстань від точки \(A\) до прямої \(B_1C_1\)
Варіант відповіді:
$$\left|\begin{array}{c}А &Б & В & Г & Д\\
1 \text{ см} & 2 \text{ см} & \sqrt{2} \text{ см} & 3 \text{ см} & 1,5 \text{ см} \end{array}\right|$$
Рішення:
Расстояние между точкой и прямой - длина перпендикуляра, опущенного из этой точки на прямую. Т.к. в задании куб,т.е. все грани перпендикулярны, то перпендикуляр к прямой \(B_1C_1\) из вершины \(A\) будет лежать на грани \(ABA_1B_1\), т.е. это будет отрезок \(AB_1\), который является диагональю квадрата. Длину \(AB_1\) можно найти из прямоугольного треугольника \(ΔABB_1\), который является равнобедренным, получаем \(AB_1 = \sqrt{AB^2 + BB_1^2} = \sqrt{1+1} = \sqrt{2}\)
Відповідь: \(В\)

