Завдання: Укажіть правильну нерівність, якщо \(a = \sin(120^0), \quad b = \cos(120^0)\)
Варіант відповіді:
$$\left|\begin{array}{c}А &Б & В & Г & Д\\
0 < a < b & a < 0 < b & a < b < 0 & b < 0 < a & 0 < b < a \end{array}\right|$$
Рішення:
1. метод. Рассмотрим единичную окружность, центр которой находится в начале координат точке \(O(0;0)\). Получим точка \(P_{\beta}\) путем поворота точки \(P(1;0)\) против часовой стрелки на угол \(\beta = 120^0\), тогда координаты этой точки будут \(x = \cos(120^0) = b; \quad y = \sin(120^0) = a\) , т. е. \(P_{\beta}(\cos(120^0);\sin(120^0))\). Из рисунка видно, что \(x = b < 0; \quad y = a > 0\) т.е. получаем \( b < 0 < a\). Этому условию отвечает ответ \(Г\)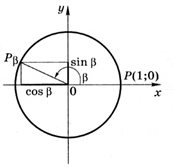
2. метод. Используем для решения таблицу приведения, получим
\( \sin(120^0) = \sin(180^0 - 60^0) = \sin(60^0)\)
\( \cos(120^0) = \cos(180^0 - 60^0) = -\cos(60^0)\)
согласно таблицы значений тригонометрических углов получим
\(\sin(60^0) = \frac{\sqrt{3}}{2}\) , тогда \(a = \frac{\sqrt{3}}{2}\)
\( -\cos(60^0) = -\frac{1}{2}\) , тогда \(b = - \frac{1}{2}\),
т.е. получаем \( b < 0 < a\)
Этому условию отвечает ответ \(Г\)
Відповідь: \(Г\)

