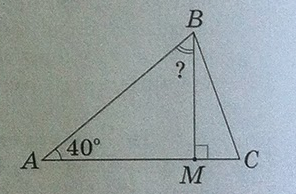
–Ч–∞–≤–і–∞–љ–љ—П: –£ —В—А–Є–Ї—Г—В–љ–Є–Ї—Г \(ABC\) –њ—А–Њ–≤–µ–і–µ–љ–Њ –≤–Є—Б–Њ—В—Г \(BM\) (–і–Є–≤. —А–Є—Б—Г–љ–Њ–Ї). –Т–Є–Ј–љ–∞—З—В–µ –≥—А–∞–і—Г—Б–љ—Г –Љ—Ц—А—Г –Ї—Г—В–∞ \(MBA\), —П–Ї—Й–Њ \(\angle A = 40^0\)
–Т–∞—А—Ц–∞–љ—В –≤—Ц–і–њ–Њ–≤—Ц–і—Ц:
$$\left|\begin{array}{c}–Р &–С & –Т & –У & –Ф\\
20^0 & 45^0 & 50^0 & 60^0 & 90^0 \end{array}\right|$$
–†—Ц—И–µ–љ–љ—П:¬†
–°—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ \(180^0\)
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ \(ABM\). –≠—В–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —В.–µ. –µ–≥–Њ —Г–≥–Њ–ї \(\angle M = 90^0\), —В–Њ–≥–і–∞ –њ–Њ–ї—Г—З–∞–µ–Љ $$\angle A + \angle B + \angle M = 180^0 => \angle B = 180^0 - \angle A - \angle M => $$ –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Є–Ј–≤–µ—Б—В–љ—Л–µ —Г–≥–ї—Л $$\angle B = 180^0 - 40^0 - 90^0 = 50^0$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: \(–Т\)
¬† –њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 1 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 3

