Завдання: Обисліть площу фігури, обмеженої графіком функції \(y = \frac{22}{3} - (x+1)^2\) і прямими \(у = \frac{x}{3}\), \(х = -1\) та \(x = 1\).
Рішення: для решения задачи необходимо построить графики функции и понять площадь какой фигуры будем искать. Смотрим рисунок.
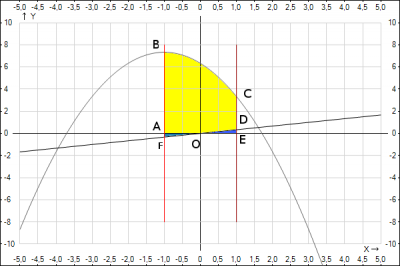
Из рисунка видно, что площадь, ограниченная кривыми, заданными в условии задания - фигура \(FBCD\). Площадь данной фигуры находится как разность площадей фигур \(ABCE\) - фигура ограниченная графиком \(y = \frac{22}{3} - (x+1)^2\), прямыми \(х = -1\) и \(x = 1\) и осью \(Ox\) и фигуры \(ODE\) - фигура ограниченная графиком \(у = \frac{x}{3}\), прямой \(x = 1\) и осью \(Ox\) плюс площадь фигуры \(AOF\) - фигура ограниченная графиком \(у = \frac{x}{3}\), прямой \(x = -1\) и осью \(Ox\) . Из рисунка видно, что две фигуры \(AOF\) и \(ODE\) - прямоугольные треугольники, которые равны (равны стороны \(AO = OD = 1\), углы \(\angle AOF = \angle DOE\) и прямые углы \(\angle A = \angle E\)), площади этих прямоугольных треугольников равны. Т.е. получаем, что площадь \(S_{FBCD} = S_{ABCE}\) и равна определенному интегралу \(\int_{-1}^{1}( \frac{22}{3} - (x+1)^2)dx\) $$S_{FBCD} = S_{ABCE} = \int_{-1}^{1}( \frac{22}{3} - (x+1)^2)dx = $$$$= \frac{22}{3}x - \frac{(x+1)^3}{3}|_{-1}^1 = $$Подставляем в полученное выражение значения верхней и нижней границы $$= \frac{22}{3}*1 - \frac{(1+1)^3}{3} - (\frac{22}{3}(-1) - \frac{(-1+1)^3}{3}) = $$$$= \frac{22}{3} - \frac{8}{3} + \frac{22}{3} = 12 =>$$$$S_{FBCD} = 12$$
Відповідь: 12

