Завдання: У прямокутний трикутник АВС вписано коло, яке дотикається катетів АС та ВС у точках K і М відповідно. Знайдіть радіус кола, описаного навколо трикутника АВС (у см), якщо АК = 4,5 см, МВ = 6 см.
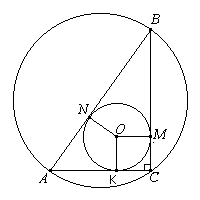
Рішення: Рассмотрим рисунок и определимся с радиусом описанной окружности. Вспомним свойство прямоугольного треугольника: середина гипотенузы прямоугольного треугольника является центром описанной около треугольника окружности, т.е. для решения задачи нужно найти гипотенузу треугольника. Рассмотрим \(ΔABC\) и вписанную окружность. \(BM = MN\), \(AN = AK\) как отрезки касательных угла к окружности, вписанной в этот угол. Докажем это: если соединить точки \(B\) и \(O\), то получим два равных прямоугольных треугольника \(ΔNBO\) и \(ΔBOM\). Из равенства прямоугольных треугольников (равны катеты \(NO = MO\) и общая гипотенуза \(BO\)) следует равенство сторон \(BM = MN\), аналогично доказывается равенство \(AN = AK\) из равенства прямоугольных треугольников \(ΔAON\) и \(ΔAOK\). Теперь можно найти гипотенузу $$AB = AN + NB = AK + BM = 4,5 + 6 = 10,5$$ Из того, что гипотенуза равна диаметру описанной окружности получим $$AB = d = 2r = 10,5 => r = \frac{10,5}{2} = 5,25$$
Відповідь: 5,25

