Завдання: Установіть відповідність між тілом обертання, заданим умовою (1-4), та формулою (А-Д) для обчислення його об’єму \(V\).
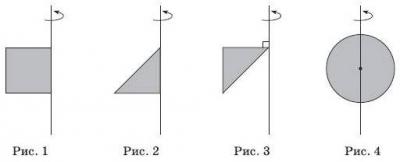
\begin{array}{|l|c|} \hline \\ 1.\quad квадрат\quad зі\quad стороною\quad а\quad обертається\quad навколо\quad прямої,\\ \quad що\quad проходить\quad через\quad сторону\quad цього\quad квадрата\quad (рис. 1) & А \quad V = \frac{1}{3}\pi \alpha^3 \\ \hline \\ 2.\quad прямокутний\quad рівнобедрений\quad трикутник\quad із\quad катетом\quad а\\ \quad обертається\quad навколо\quad прямої, \quad що\quad проходить\quad через\\ \quad катет\quad цього\quad трикутника\quad (рис. 2) & Б \quad V = \frac{9}{16}\pi \alpha^3 \\ \hline \\ 3.\quad прямокутний\quad рівнобедрений\quad трикутник\quad із катетом\quad а\\ \quad обертається\quad навколо\quad прямої,\quad що\quad проходить\quad через\\ \quad вершину\quad гострого\quad кута\quad цього\quad трикутника\quad перпендикулярно\\ \quad до\quad одного\quad з\quad його\quad катетів\quad (рис. 3) & В \quad V = \frac{2}{3}\pi \alpha^3 \\ \hline \\ 4.\quad круг,\quad радіус\quad якого\quad дорівнює\quad \frac{3}{4}а, \quad обертається\quad навколо\\ \quad прямої\quad що\quad проходить\quad через\quad центр\quad цього\quad круга\quad (рис. 4) & Г \quad V = \pi \alpha^3 \\ \hline \\ & Д \quad V = 2 \pi \alpha^3 \\ \hline \end{array}
Рішення:
1. квадрат зі стороною \(а\) обертається навколо прямої, що проходить через сторону цього квадрата (рис. 1)
При вращении квадрат (рис.1) получаем тело вращения - цилиндр. Объем цилиндра находится по формуле \(V_{цил} = S_{осн}h_{цил} = \pi r^2 * h\), где радиус круга основания равен стороне квадрата \(r = a\), высота цилиндра также равна стороне квадрата \(h = a\). Подставляем в формулу объема цилиндра $$V_{цил} = \pi a^3$$
Відповідь: 1 -> Г, \(V = \pi a^3\)
2. прямокутний рівнобедрений трикутник із катетом \(а\) обертається навколо прямої, що проходить через катет цього трикутника (рис. 2)
При вращении равнобедренного прямоугольного треугольника (рис.2) получаем тело вращения - конус. Объем конуса находится по формуле \(V_{кон} = \frac{1}{3}S_{осн}h_{кон} = \frac{1}{3} \pi r^2 * h\), где радиус круга основания равен катету равнобедренного прямоугольного треугольника \(r = a\), высота конуса также равна катету \(h = a\). Подставляем в формулу объема конуса $$V_{кон} = \frac{1}{3} \pi a^3$$
Відповідь: 2 -> А, \(V = \frac{1}{3} \pi a^3\)
3. прямокутний рівнобедрений трикутник із катетом \(а\) обертається навколо прямої, що проходить через вершину гострого кута цього трикутника перпендикулярно до одного з його катетів (рис. 3)
При вращении равнобедренного прямоугольного треугольника (рис.3) получаем тело вращения - цилиндр середина которого вырезана в форме конуса. Объем фигуры нужно находить как разность объема цилиндра и конуса. Формулы объемов были получены в п.1 и п.2, тогда искомый объем равен \(V = \pi a^3 - \frac{1}{3} \pi a^3 = >\) $$\frac{2}{3} \pi a^3$$
Відповідь: 3 -> В, \(V = \frac{2}{3} \pi a^3\)
4. круг, радіус якого дорівнює 3/4а, обертається навколо прямої що проходить через центр цього круга (рис. 4)
При вращении круга (рис.4) получаем тело вращения - шар.Объем шара находится по формуле \(V_{шара} = \frac{4}{3}\pi r^3\). Подставляем радиус круга \(r = \frac{3}{4}a\) в формулу, получаем \(V_{шара} = \frac{4}{3}\pi (\frac{3}{4}a)^3 =>\) $$V_{шара} = \frac{9}{16}\pi a^3$$
Відповідь: 4 -> Б, \(V = \frac{9}{16}\pi a^3\)

