–Ч–∞–≤–і–∞–љ–љ—П: –Ю—Б–љ–Њ–≤–Њ—О –њ—Ц—А–∞–Љ—Ц–і–Є \(SABCD\)¬† —Ф —В—А–∞–њ–µ—Ж—Ц—П \(ABCD\) ¬† \((ADвИ•BC)\),¬† –і–Њ–≤–ґ–Є–љ–∞ —Б–µ—А–µ–і–љ—М–Њ—Ч –ї—Ц–љ—Ц—Ч —П–Ї–Њ—Ч –і–Њ—А—Ц–≤–љ—О—Ф 5 —Б–Љ. –С—Ц—З–љ–µ —А–µ–±—А–Њ \(SB\)¬† –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–µ –і–Њ –њ–ї–Њ—Й–Є–љ–Є –Њ—Б–љ–Њ–≤–Є –њ—Ц—А–∞–Љ—Ц–і–Є —Ц –≤–і–≤—Ц—З—Ц –±—Ц–ї—М—И–µ –≤—Ц–і —Б–µ—А–µ–і–љ—М–Њ—Ч –ї—Ц–љ—Ц—Ч —В—А–∞–њ–µ—Ж—Ц—Ч \(ABCD\).
–Ч–љ–∞–є–і—Ц—В—М –≤—Ц–і—Б—В–∞–љ—М –≤—Ц–і —Б–µ—А–µ–і–Є–љ–Є —А–µ–±—А–∞ \(SD\)¬† –і–Њ –њ–ї–Њ—Й–Є–љ–Є \(SBC\)¬† (—Г —Б–Љ), —П–Ї—Й–Њ –Њ–±'—Ф–Љ –њ—Ц—А–∞–Љ—Ц–і–Є –і–Њ—А—Ц–≤–љ—О—Ф \(240 —Б–Љ^3\).
–†—Ц—И–µ–љ–љ—П: —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–Є—Б—Г–љ–Њ–Ї
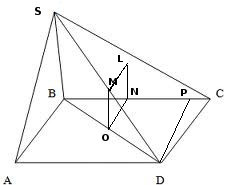
–†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –і–Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є —А–∞–≤–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А—Г, –Њ–њ—Г—Й–µ–љ–љ–Њ–Љ—Г –Є–Ј —В–Њ—З–Ї–Є –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В—М. –Я—А–Њ–≤–µ–і–µ–Љ –њ–ї–Њ—Б–Ї–Њ—Б—В—М —З–µ—А–µ–Ј —В. \(M\) –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є \(SBC\) –Є –њ—А—П–Љ–Њ–є \(BC\), –ї–µ–ґ–∞—Й–µ–є –≤ —Н—В–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є. –Э–∞–є–і–µ–Љ –і–ї–Є–љ—Г –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–∞ –Є–Ј —В. \(M\)¬† - \(ML\) –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В—М \(SBC\). –Я—А–Њ–≤–µ–і–µ–Љ –њ–ї–Њ—Б–Ї–Њ—Б—В—М \(SBD\) –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–µ—З–µ–љ–Є–µ \(ќФSBD\).¬† –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї \(OMLN\), –њ–Њ–ї—Г—З–µ–љ–љ—Л–є –њ–µ—А–µ—Б–µ—З–µ–љ–Є–µ–Љ —Н—В–Є—Е –њ–ї–Њ—Б–Ї–Њ—Б—В–µ–є - –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –њ–Є—А–∞–Љ–Є–і–∞ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–∞—П). –Ґ.–µ. \(ML = ON\). \(MO\) - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П \(ќФSBD\). –Ю–њ—Г—Б—В–Є–Љ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А \(DP\) –Є–Ј –≤–µ—А—И–Є–љ—Л \(D\) –љ–∞ —Б—В–Њ—А–Њ–љ—Г \(BC\). –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї \(ќФBDP\). \(ON\) - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФBDP\), –≥–і–µ \(DP\) - –≤—Л—Б–Њ—В–∞ —В—А–∞–њ–µ—Ж–Є–Є, —В.–µ. \(ON = \frac{DP}{2}\).
–Ф–ї—П —А–µ—И–µ–љ–Є–Є –Ј–∞–і–∞—З–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –љ–∞–є—В–Є –≤—Л—Б–Њ—В—Г —В—А–∞–њ–µ—Ж–Є–Є. –Э–∞–є–і–µ–Љ –µ–µ –Є—Б–њ–Њ–ї—М–Ј—Г—П –Є–Ј–≤–µ—Б—В–љ—Л–є –Њ–±—К–µ–Љ —В—А–∞–њ–µ—Ж–Є–Є –Є —Д–Њ—А–Љ—Г–ї—Г –Њ–±—К–µ–Љ–∞ $$V_{–њ–Є—А} = \frac{1}{3}S_{–Њ—Б–љ.}*H_{–њ–Є—А} = \frac{1}{3} \frac{a+b}{2}*h_{—В—А.}*H_{–њ–Є—А} $$–Ш–Ј —Г—Б–ї–Њ–≤–Є—П –Є–Ј–≤–µ—Б—В–љ–∞ –і–ї–Є–љ–∞ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–∞–њ–µ—Ж–Є–Є, –Ї–Њ—В–Њ—А–∞—П —А–∞–≤–љ–∞ \(\frac{a+b}{2} = 5\) –Є –≤—Л—Б–Њ—В–∞ –њ–Є—А–∞–Љ–Є–і—Л \(H_{–њ–Є—А} = 2*5 = 10\). –Я–Њ–і—Б—В–∞–≤–Є–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –≤ —Д–Њ—А–Љ—Г–ї—Г –Є –љ–∞–є–і–µ–Љ –≤—Л—Б–Њ—В—Г —В—А–∞–њ–µ—Ж–Є–Є $$V_{–њ–Є—А} = \frac{1}{3}*\frac{a+b}{2}*h_{—В—А.}*H_{–њ–Є—А} = \frac{1}{3}*5*h_{—В—А.}*10 = 240 => h_{—В—А.} = \frac{72}{5}$$–Э–∞–є–і–µ–Љ –Є—Б–Ї–Њ–Љ–Њ–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –і–Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є $$ML = ON = \frac{1}{2} h_{—В—А} = \frac{1}{2}*\frac{72}{5} = \frac{36}{5} = 7,2$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 7,2
 
¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 31 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 33

