Завдання: Установіть відповідність між твердженням (1-4) та функцією (А-Д), для якої це твердження є правильним.
\begin{array}{|l|c|} \hline \\ Твердження & Функція \\ \hline \\ 1.\quad графік\quad функції\quad не\quad перетинає \quad жодну\quad з\quad осей\quad координат & А \quad y = -x+2 \\ \hline \\ 2.\quad областю\quad значень\quad функції\quad є\quad проміжок\quad (0; +\infty) & Б \quad y = x^2-2 \\ \hline \\ 3.\quad функція\quad спадає\quad на\quad всій\quad області\quad визначення & В \quad y = -\frac{1}{x} \\ \hline \\ 4.\quad на\quad відрізку\quad [-1,5;1,5] \quad функція\quad має\quad два\quad нулі & Г \quad y = 3^x \\ \hline \\ & Д \quad y = \cos x \\ \hline \end{array}
Рішення:
1. графік функції не перетинає жодну з осей координат
Точки пересечения с осью \(x\) это точки у которых \(y = 0\) и наоборот, точки пересечения с осью \(y\) это точки у которых \(x = 0\). Нам необходимо найти функцию, которая не пересекает оси, подставляем в функцию \(x =0\) и ищем функцию у которой \(y\) не существует, подставляем в функцию \(y =0\) и ищем функцию у которой \(x\), не существует. Из приведенных функций только функция \(y = -\frac{1}{x} \) => \(D_f = x \ne 0\) => \( x = -\frac{1}{y}\) =>\(E_f = y \ne 0\) не имеет точек пересечения с осями
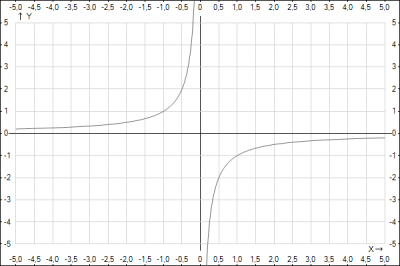
Відповідь: \(1 -> В \quad y = -\frac{1}{x} \)
2. областю значень функції є проміжок \(0; +\infty\)
Область значений показательной функции: \(E (y)=R+\) - множество всех положительных чисел.
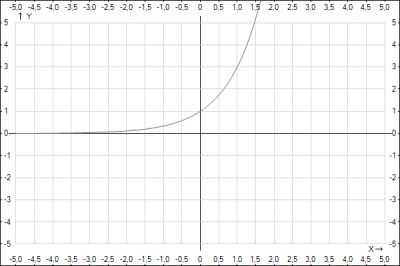
Відповідь: \(2 -> Г \quad y = 3^x \)
3. функція спадає на всій області визначення
Функция называется убывающей если большему \(x\) - соответствует меньший \(y\). Из оставшихся функций такой является \(y = -x+2\). Например: \(f(0) = 2\), \(f(2) = 0\)
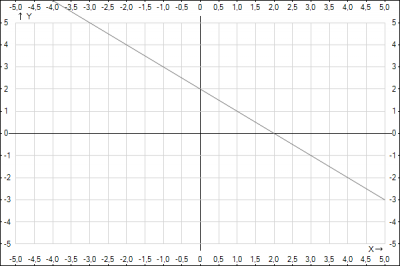
Відповідь: \(3 -> А \quad y = -x+2 \)
4. на відрізку \([-1,5;1,5]\) функція має два нулі
Нужна функция у которой на заданном отрезке есть две точки пересечения с осью \(Ox\), т.е. при y =0. Это может быть либо степенная функция \(y = x^2-2\). Проверим это. Найдем корни квадратного уравнения \(x^2 - 2 = 0 => x = \pm \sqrt{2} \approx \pm 1,414\). Функция удовлетворяет заданию.
Проверим, на всякий случай, и тригонометрическую функцию \(y = \cos x = 0 => x = \pm \pi n, n \in Z\). Проверяем, при \(n=1, x = \pi \approx 3,14\) - в интервал не попал, т.е. функция не подходит.
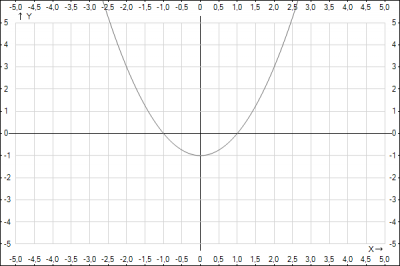
Відповідь: \(4 -> Б \quad y = x^2 - 2 \)

