–Ч–∞–≤–і–∞–љ–љ—П:¬† –і–ї—П —А–Њ–Ј—Ц–≥—А—Ц–≤–∞–љ–љ—П –≤ –Љ—Ц–Ї—А–Њ—Е–≤–Є–ї—М–Њ–≤—Ц–є –њ–µ—З—Ц —А—Ц–і–Ї–Є—Е —Б—В—А–∞–≤ –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—В—М –њ–Њ—Б—Г–і—Г —Г —Д–Њ—А–Љ—Ц —Ж–Є–ї—Ц–љ–і—А–∞, —А–∞–і—Ц—Г—Б –Њ—Б–љ–Њ–≤–Є —П–Ї–Њ–≥–Њ –і–Њ—А—Ц–≤–љ—О—Ф 9 —Б–Љ. –Я–Њ—Б—Г–і–Є–љ–∞ —Б—В–∞–≤–Є—В—М—Б—П –љ–∞ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Є–є –і–Є—Б–Ї —Г —Д–Њ—А–Љ—Ц –Ї—А—Г–≥–∞ —Ц –љ–∞–Ї—А–Є–≤–∞—Ф—В—М—Б—П –Ї—А–Є—И–Ї–Њ—О, —Й–Њ –Љ–∞—Ф —Д–Њ—А–Љ—Г –њ—Ц–≤—Б—Д–µ—А–Є (–і–Є–≤. —А–Є—Б—Г–љ–Њ–Ї). –†–∞–і—Ц—Г—Б –њ—Ц–≤—Б—Д–µ—А–Є –і–Њ—А—Ц–≤–љ—О—Ф 12 —Б–Љ —Ц —Ф –Љ–µ–љ—И–Є–Љ –Ј–∞ —А–∞–і—Ц—Г—Б –Ї—А—Г–≥–∞. –£–Ї–∞–ґ—Ц—В—М –љ–∞–є–±—Ц–ї—М—И–µ –Ј –љ–∞–≤–µ–і–µ–љ–Є—Е –Ј–љ–∞—З–µ–љ—М, —П–Ї–Њ–Љ—Г –Љ–Њ–ґ–µ –і–Њ—А—Ц–≤–љ—О–≤–∞—В–Є –≤–Є—Б–Њ—В–∞ –њ–Њ—Б—Г–і–Є–љ–Є, —П–Ї—Й–Њ –њ–Њ—Б—Г–і–Є–љ–∞ –љ–µ —В–Њ—А–Ї–∞—Ф—В—М—Б—П –Ї—А–Є—И–Ї–Є.
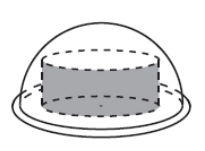
\begin{array}{|c|c|c|—Б|c|} \hline \\¬†–Р & –С &¬† –Т &¬† –У &¬† –Ф \\ \hline¬† \\ 3cm &¬† 5 cm &¬† 6 cm & 7 cm & 8 cm\\ \hline \end{array}
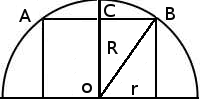
–†—Ц—И–µ–љ–љ—П: –њ—А–Њ–≤–µ–і–µ–Љ –Њ—Б–µ–≤–Њ–µ —Б–µ—З–µ–љ–Є–µ —Ж–Є–ї–Є–љ–і—А–∞. –Т —Б–µ—З–µ–љ–Є–Є –њ–Њ–ї—Г—З–Є–Љ –њ–Њ–ї—Г–Ї—А—Г–≥ –Є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Ш–Ј –Ј–∞–і–∞–љ–Є—П —Б–ї–µ–і—Г–µ—В, —З—В–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –љ–∞–є—В–Є –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ—Г—О –≤—Л—Б–Њ—В—Г —Ж–Є–ї–Є–љ–і—А–∞, —В.–µ. –≤ —А–∞–Ј—А–µ–Ј–µ - –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ—Г—О –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ \(CO\), –Ї–Њ—В–Њ—А—Л–є —А–∞–≤–µ–љ —Б—В–Њ—А–Њ–љ–µ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —А–∞–і–Є—Г—Б —Б—Д–µ—А—Л R, –∞ —А–∞–і–Є—Г—Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П —Ж–Є–ї–Є–љ–і—А–∞ r.¬† –Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ќФOCB –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ –љ–∞–є–і–µ–Љ \(OC = \sqrt{OB^2-CB^2} = \sqrt{R^2-r^2} = \sqrt{12^2-9^2} = \sqrt{63} \). –°–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞–љ–Є—П —Ж–Є–ї–Є–љ–і—А –љ–µ –Ї–∞—Б–∞–µ—В—Б—П —Б—Д–µ—А—Л,—В.–µ. \(OC < \sqrt{63} \approx 7,9 \). –Т—Л–±–Є—А–∞–µ–Љ –Є–Ј –Њ—В–≤–µ—В–Њ–≤ –љ–∞–Є–±–Њ–ї—М—И–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –≤—Л—Б–Њ—В—Л –њ–Њ—Б—Г–і–Є–љ—Л –Љ–µ–љ—М—И–µ–µ 7,9. –Ю—В–≤–µ—В 7.
–Т—Ц–і–њ–Њ–≤—Ц–і—М: \(–У -> 7 cm\)
 
¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 19 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 21

