Зовнішнє незалежне оцінювання 2012 року з математики (1 сесія). Завдання № 24.

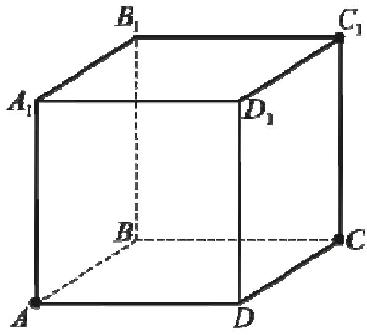
Зміст завдання : На рисунку зображено куб  $ABCDA_{1}B_{1}C_{1}D_{1}$. До кожного початку речення (1-4) доберіть його закінчення (А-Д) так, щоб урворилося правильне твердження.

Рішення:

У завданні розглядається площину $AA_{1}B_{1}B$ і прямі, що проходять через ребра і вершини куба. Приступимо до розгляду завдання

1. Пряма $CB$ - перпендикулярна площині $AA_{1}B_{1}B$ і має з нею спільну 1 точку (за визначенням куба)- відповідь Б перпендикулярна площині $AA_{1}B_{1}B$.
2. Пряма $CD_{1}$ - лежить у площині $DD_{1}C_{1}C$ , яка паралельна площині $AA_{1}B_{1}B$ (за визначенням куба) , тобто теж палаллельна  площині  $AA_{1}B_{1}B$ - відповідь A паралельна площині $AA_{1}B_{1}B$.
3. Пряма $АС$ лежить у площині $ABCD$, яка перпендикулярна площині $AA_{1}B_{1}B$ (за визначенням куба). Пряма $AB$ є перетином двох плосокслей. Пряма $АС$ лежить на діагоналі квадрата $ABCD$, обто кут між діагоналлю квадрата та стороною  $AB$ дорівнює $45^0$, так як дві площини перпендикулярні, то кут між прямою і площиною також дорівнює $45^0$ -  відповідь Д утворює з площиною $AA_{1}B_{1}B$ кут $45^0$.
4. Пряма $A_{1}B$ - належить площині $AA_{1}B_{1}B$.

Відповідь: