1. –Ы—Ц–љ—Ц–є–љ–∞ –Љ–Њ–і–µ–ї—М –≤–Є—В—А–∞—В. –Ґ–Њ—З–Ї–∞ –±–µ–Ј–Ј–±–Є—В–Ї–Њ–≤–Њ—Б—В—Ц.
–Я—А–Є –≤–Є—А–Њ–±–љ–Є—Ж—В–≤—Ц x –Њ–і–Є–љ–Є—Ж—М –±—Г–і—М-—П–Ї–Њ—Ч –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч –Ј–∞–≥–∞–ї—М–љ—Ц –≤–Є—В—А–∞—В–Є \(C(x)\) —Б–Ї–ї–∞–і–∞—О—В—М—Б—П —Ц–Ј –њ–Њ—Б—В—Ц–є–љ–Є—Е (—Д—Ц–Ї—Б–Њ–≤–∞–љ–Є—Е) –≤–Є—В—А–∞—В \(F\); –Ј–Љ—Ц–љ–љ–Є—Е –≤–Є—В—А–∞—В \(V\), —В–Њ–±—В–Њ –Љ–∞—Ф–Љ–Њ: $$ C=F+V$$
–Я–Њ—Б—В—Ц–є–љ—Ц –≤–Є—В—А–∞—В–Є \(F\) вИТ —Ж–µ –≤–Є—В—А–∞—В–Є, —Й–Њ –љ–µ –Ј–∞–ї–µ–ґ–∞—В—М –≤—Ц–і —З–Є—Б–ї–∞ –Њ–і–Є–љ–Є—Ж—М –≤–Є—А–Њ–±–ї–µ–љ–Њ—Ч –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч. –Т–Њ–љ–Є –Љ—Ц—Б—В—П—В—М —Г —Б–Њ–±—Ц –∞–Љ–Њ—А—В–Є–Ј–∞—Ж—Ц—О, –Њ—А–µ–љ–і—Г –њ—А–Є–Љ—Ц—Й–µ–љ–љ—П, –≤—Ц–і—Б–Њ—В–Ї–Є –њ–Њ –њ–Њ–Ј–Є–Ї–∞—Е —Ц —В.–њ.¬†
–Ч–Љ—Ц–љ–љ—Ц –≤–Є—В—А–∞—В–Є¬†\(V\)¬†вИТ —Ж–µ –≤–Є—В—А–∞—В–Є, —Й–Њ –њ—А—П–Љ–Њ –Ј–∞–ї–µ–ґ–∞—В—М –≤—Ц–і –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц –≤–Є—А–Њ–±–ї–µ–љ–Њ—Ч –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч. –Т–Њ–љ–Є –Љ—Ц—Б—В—П—В—М —Г —Б–Њ–±—Ц –≤–∞—А—В—Ц—Б—В—М —Б–Є—А–Њ–≤–Є–љ–Є, —А–Њ–±–Њ—З–Њ—Ч —Б–Є–ї–Є –є —В.–њ.
–£ –љ–∞–є–њ—А–Њ—Б—В—Ц—И–Њ–Љ—Г –≤–Є–њ–∞–і–Ї—Г –Ј–Љ—Ц–љ–љ—Ц –≤–Є—В—А–∞—В–Є –њ—А—П–Љ–Њ –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц \(X\) вИТ –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц –≤–Є—А–Њ–±–ї–µ–љ–Њ—Ч –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч. –Ъ–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ–Њ—Б—В—Ц \(–Р\) вИТ —Ж–µ –Ј–Љ—Ц–љ–љ—Ц –≤–Є—В—А–∞—В–Є –њ–Њ –≤–Є—А–Њ–±–љ–Є—Ж—В–≤—Г –Њ–і–љ—Ц—Ф—Ч –Њ–і–Є–љ–Є—Ж—Ц –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч \(V=ax \).
–ѓ–Ї—Й–Њ –њ–Њ–Ј–љ–∞—З–Є—В–Є —З–µ—А–µ–Ј \(b\) —Д—Ц–Ї—Б–Њ–≤–∞–љ—Ц –≤–Є—В—А–∞—В–Є, —В–Њ –≤–Є–є–і–µ —А—Ц–≤–љ—П–љ–љ—П, —Й–Њ –љ–∞–Ј–Є–≤–∞—О—В—М –ї—Ц–љ—Ц–є–љ–Њ—О –Љ–Њ–і–µ–ї–ї—О –≤–Є—В—А–∞—В: $$C(x)=b+ax$$¬†–°—Г–Ї—Г–њ–љ–Є–є –і–Њ—Е—Ц–і \(R(x)\) , –Њ–і–µ—А–ґ—Г–≤–∞–љ–Є–є –њ—Ц–і–њ—А–Є—Ф–Љ—Б—В–≤–Њ–Љ –≤—Ц–і –њ—А–Њ–і–∞–ґ—Г x–Њ–і–Є–љ–Є—Ж—М –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч, –≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П —Д–Њ—А–Љ—Г–ї–Њ—О: $$R(x) = px$$¬†–і–µ \(p\) вФА —Ж—Ц–љ–∞ –Њ–і–Є–љ–Є—Ж—Ц —В–Њ–≤–∞—А—Г.
–ѓ–Ї—Й–Њ –≤–Є—А–Њ–±–ї–µ–љ–Њ –є –њ—А–Њ–і–∞–љ–Њ x –Њ–і–Є–љ–Є—Ж—М –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч, —В–Њ –њ—А–Є–±—Г—В–Њ–Ї \(P(x)\)¬†–≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П —Д–Њ—А–Љ—Г–ї–Њ—О: $$P(x) = R(x) -C(x) $$¬†–Ґ–Њ—З–Ї–∞, –≤ —П–Ї—Ц–є –њ—А–Є–±—Г—В–Њ–Ї –њ–µ—А–µ—В–≤–Њ—А—О—Ф—В—М—Б—П –≤ –љ—Г–ї—М, –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –Ї—А–∞–њ–Ї–Њ—О –±–µ–Ј–Ј–±–Є—В–Ї–Њ–≤–Њ—Б—В—Ц.
–Я—А–Є–Ї–ї–∞–і 1.–Т—Ц–і–Њ–Љ–Њ, —Й–Њ —Д—Ц–Ї—Б–Њ–≤–∞–љ—Ц –≤–Є—В—А–∞—В–Є –≤–Є—А–Њ–±–љ–Є—Ж—В–≤–∞ —Б—В–∞–љ–Њ–≤–ї—П—В—М 10 —В–Є—Б. –≥—А–љ. –љ–∞ –Љ—Ц—Б—П—Ж—М, –Ј–Љ—Ц–љ–љ—Ц –≤–Є—В—А–∞—В–Є 30 –≥—А–љ. –љ–∞ –Њ–і–Є–љ–Є—Ж—О –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч, –≤–Є—В–Њ—А–≥ 50 –≥—А–љ. –Ј–∞ –Њ–і–Є–љ–Є—Ж—О –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч. –Я–Њ—В—А—Ц–±–љ–Њ —Б–Ї–ї–∞—Б—В–Є —Д—Г–љ–Ї—Ж—Ц—О –њ—А–Є–±—Г—В–Ї—Г –є –њ–Њ–±—Г–і—Г–≤–∞—В–Є —Ч—Ч –≥—А–∞—Д—Ц–Ї.
–†–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞–љ–љ—П. –Ч–∞ —Г–Љ–Њ–≤–Њ—О –Ј–∞–і–∞—З—Ц –њ–Њ—Б—В—Ц–є–љ—Ц –≤–Є—В—А–∞—В–Є F =10 000. –Ю—Б–Ї—Ц–ї—М–Ї–Є –Ј–Љ—Ц–љ–љ—Ц –≤–Є—В—А–∞—В–Є –њ–Њ –≤–Є—А–Њ–±–љ–Є—Ж—В–≤—Г –Њ–і–љ—Ц—Ф—Ч –Њ–і–Є–љ–Є—Ж—Ц –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч —Б—В–∞–љ–Њ–≤–ї—П—В—М 30 –≥—А–љ. (a = 30), —В–Њ –Ј–Љ—Ц–љ–љ—Ц –≤–Є—В—А–∞—В–Є, —Й–Њ –Ј–∞–ї–µ–ґ–∞—В—М –≤—Ц–і –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц –≤–Є—А–Њ–±–ї–µ–љ–Њ—Ч –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч, ¬†\(V = 30 x\)¬†
–і–µ \(x\) ¬†ћґ ¬†–Ї—Ц–ї—М–Ї—Ц—Б—В—М –≤–Є—А–Њ–±–ї–µ–љ–Њ—Ч –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч.¬†
–Ґ–∞–Ї–Є–Љ —З–Є–љ–Њ–Љ, –Ј–∞–≥–∞–ї—М–љ—Ц –≤–Є—В—А–∞—В–Є —Б—В–∞–љ–Њ–≤–ї—П—В—М $$C(x) =10000 + 30x $$
–°—Г–Ї—Г–њ–љ–Є–є –і–Њ—Е—Ц–і, –≤—Ц–і –њ—А–Њ–і–∞–ґ—Г x –Њ–і–Є–љ–Є—Ж—М –њ—А–Њ–і—Г–Ї—Ж—Ц—Ч, –≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П —В–∞–Ї–Є–Љ —З–Є–љ–Њ–Љ $$R(x) = 50 x$$
–Я–Њ–±—Г–і—Г—Ф–Љ–Њ –≥—А–∞—Д—Ц–Ї–Є —Д—Г–љ–Ї—Ж—Ц–є –і–Њ—Е–Њ–і—Г –є –≤–Є—В—А–∞—В:¬†
 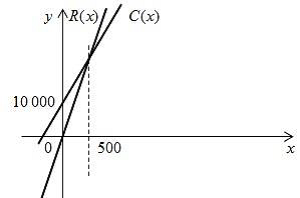
–†–Є—Б. 1
–Ґ–Њ—З–Ї—Г –њ–µ—А–µ—В–Є–љ—Г –њ—А—П–Љ–Є—Е ¬†\(C(x) =10000 + 30x\) —В–∞ ¬†\(R(x) = 50 x \) ¬†–Ј–љ–∞–є–і–µ–Љ–Њ —В–∞–Ї–Є–Љ —З–Є–љ–Њ–Љ: ¬† \(C(x) = R(x)\) ,¬†—В–Њ–і—Ц ¬† \(10000+30x = 50x\) ¬† –Њ—В–ґ–µ, ¬† \(x = 500, C(x) = R(x) = 25000\)
–Я—А–Є–±—Г—В–Њ–Ї, —П–Ї—Ц–є –Њ–і–µ—А–ґ—Г—Ф –њ—Ц–і–њ—А–Є—Ф–Љ—Б—В–≤–Њ, –Љ–Њ–ґ–љ–∞ –Ј–љ–∞–є—В–Є –Ј–∞ —Д–Њ—А–Љ—Г–ї—Ц ¬†$$ P(x)= R(x) -C(x) $$ ¬†–Ґ–Њ–Љ—Г ¬†$$ P(x) = 50 x - (10000 + 30 x) = 20 x -10000 => ¬†P(x) = 20 x -10000 $$¬†
–Я–Њ–±—Г–і—Г—Ф–Љ–Њ –≥—А–∞—Д—Ц–Ї —Д—Г–љ–Ї—Ж—Ц—Ч –њ—А–Є–±—Г—В–Ї—Г. –Я—А–Є x = 500 ¬†–Љ–∞—Ф–Љ–Њ P(x) = 0.
–Ю—В–ґ–µ, –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є –њ–µ—А—И–Њ—Ч —В–Њ—З–Ї–Є (500;0). –Я—А–Є x = 600 –Љ–∞—Ф–Љ–Њ ¬†P(x) = 2000; –Њ—В—А–Є–Љ–∞–ї–Є –і—А—Г–≥—Г —В–Њ—З–Ї—Г (600; 2000). –І–µ—А–µ–Ј –і–≤—Ц —В–Њ—З–Ї–Є –љ–∞ –њ–ї–Њ—Й–Є–љ—Ц –њ—А–Њ–≤–µ–і–µ–Љ–Њ –њ—А—П–Љ—Г, —П–Ї–∞ —Ф –≥—А–∞—Д—Ц–Ї–Њ–Љ —Д—Г–љ–Ї—Ж—Ц—Ч P(x):
–†–Є—Б. 2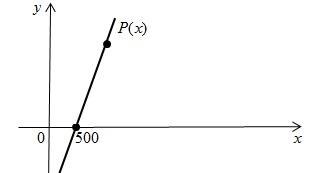
 
–ѓ–Ї –≤–Є–і–љ–Њ —Ц–Ј –≥—А–∞—Д—Ц–Ї–∞, –њ—А–Є –Ј–љ–∞—З–µ–љ–љ—П—Е x –Љ–µ–љ—И–µ 500 –њ—А–Є–±—Г—В–Њ–Ї –≤—Ц–івАЩ—Ф–Љ–љ–Є–є (–≥—А–∞—Д—Ц–Ї P(x) —А–Њ–Ј—В–∞—И–Њ–≤–∞–љ–Є–є –љ–Є–ґ—З–µ –Њ—Б—Ц Ox), —В–Њ–±—В–Њ –≤–Є—А–Њ–±–љ–Є—Ж—В–≤–Њ –Ј–±–Є—В–Ї–Њ–≤–µ. –Я—А–Є –Ј–±—Ц–ї—М—И–µ–љ–љ—Ц x –њ—А–Є–±—Г—В–Њ–Ї –Ј—А–Њ—Б—В–∞—Ф, —Г —В–Њ—З—Ж—Ц –Ј –∞–±—Б—Ж–Є—Б–Њ—О x = 500 –≤—Ц–љ –і–Њ—А—Ц–≤–љ—О—Ф –љ—Г–ї—О (—В–Њ—З–Ї–∞ –±–µ–Ј–Ј–±–Є—В–Ї–Њ–≤–Њ—Б—В—Ц) —Ц –њ—Ц—Б–ї—П —Ж—М–Њ–≥–Њ —Б—В–∞—Ф –і–Њ–і–∞—В–љ—Ц–Љ (–і–Є–≤. —А–Є—Б. 2).
–Ч–∞–і–∞—З–∞ 1.¬†–Т–Ј—Г—В—В—Ф–≤–∞ —Д–∞–±—А–Є–Ї–∞ –њ—А–Њ–і–∞—Ф —В—Г—Д–ї—Ц –Ј–∞ —Ж—Ц–љ–Њ—О 350+3*m+2*n¬†–≥—А–љ. –Ј–∞ –њ–∞—А—Г. –Т–Є—В—А–∞—В–Є —Б—В–∞–љ–Њ–≤–ї—П—В—М \(63000+100*m\)¬†–≥—А–љ. –Ј–∞ \(100+n\)¬†–њ–∞—А —В—Г—Д–µ–ї—М —В–∞ \(60750+100*m\)¬†¬†—В–Є—Б. –≥—А–љ. –Ј–∞ \(85+n\)¬†–њ–∞—А, –і–µ m=¬†2 , n¬†= 20
–Ч–∞–≤–і–∞–љ–љ—П
1) –Ч–љ–∞–є—В–Є —А—Ц–≤–љ—П–љ–љ—П –њ—А—П–Љ–Њ—Ч –≤–Є—В—А–∞—В \(C(x) = b + ax \),(—П–Ї–µ –≤ –±—Ц–ї—М—И –Ј–≤–Є—З–љ–Њ–Љ—Г –≤–Є–≥–ї—П–і—Ц –Љ–Њ–ґ–љ–∞ –њ–µ—А–µ–њ–Є—Б–∞—В–Є —В–∞–Ї —Г = b + ax), –Ј–∞ –і–≤–Њ–Љ–∞ —В–Њ—З–Ї–∞–Љ–Є y-y2 / y1-y2=x-x2 / x1-x2 ¬† ¬† ¬† (1)
2) ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†–Ч–љ–∞–є—В–Є —А—Ц–≤–љ—П–љ–љ—П –њ—А—П–Љ–Њ—Ч –і–Њ—Е–Њ–і—Г R(x) = px.
3) ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†–Я–Њ–±—Г–і—Г–≤–∞—В–Є –ї—Ц–љ—Ц—Ч C(x), R(x) —В–∞ –Ј–љ–∞–є—В–Є —В–Њ—З–Ї—Г —Ч—Е –њ–µ—А–µ—В–Є–љ—Г –Ь0 .
4) ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†–°–Ї–ї–∞—Б—В–Є —А—Ц–≤–љ—П–љ–љ—П —Д—Г–љ–Ї—Ж—Ц—Ч –њ—А–Є–±—Г—В–Ї—Г P(x) = R(x) -C(x) .
5) ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†–Я–Њ–±—Г–і—Г–≤–∞—В–Є —А—Ц–≤–љ—П–љ–љ—П —Д—Г–љ–Ї—Ж—Ц—Ч –њ—А–Є–±—Г—В–Ї—Г P(x) —В–∞ –Ј–љ–∞–є—В–Є —В–Њ—З–Ї—Г –±–µ–Ј–Ј–±–Є—В–Ї–Њ–≤–Њ—Б—В—Ц –Ь1.
6) ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†–ѓ–Ї –Љ—Ц–ґ —Б–Њ–±–Њ—О –њ–Њ–≤вАЩ—П–Ј–∞–љ—Ц –∞–±—Б—Ж–Є—Б–Є —В–Њ—З–Њ–Ї –Ь0, –Ь1?
7) ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†–°–Ї—Ц–ї—М–Ї–Є –њ–∞—А —В—Г—Д–µ–ї—М —Д–∞–±—А–Є–Ї–∞ –њ–Њ–≤–Є–љ–љ–∞ –Ј—А–Њ–±–Є—В–Є –є –њ—А–Њ–і–∞—В–Є, —Й–Њ–±
–Њ–і–µ—А–ґ–∞—В–Є 10% –і–Њ—Е–Њ–і—Г –љ–∞ –≥—А–Њ—И—Ц, –≤–Ї–ї–∞–і–µ–љ—Ц —Г –њ–Њ—Б—В—Ц–є–љ—Ц –≤–Є—В—А–∞—В–Є?
–Ч–∞–≤–і–∞–љ–љ—П 1, 2, 4, 6, 7 –≤–Є–Ї–Њ–љ—Г–≤–∞—В–Є –±–µ–Ј–Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П –Ї–Њ–Љ–њвАЩ—О—В–µ—А–∞.
–Ч–∞–≤–і–∞–љ–љ—П 3, 5 –≤–Є–Ї–Њ–љ—Г–≤–∞—В–Є –љ–∞ –Ї–Њ–Љ–њвАЩ—О—В–µ—А—Ц.
2. –Ч–∞–Ї–Њ–љ–Є –њ–Њ–њ–Є—В—Г —В–∞ –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—Ч.
–Ъ—Ц–ї—М–Ї—Ц—Б—В—М —В–Њ–≤–∞—А—Г, —Й–Њ –њ–Њ–Ї—Г–њ—Ж—Ц –њ—А–Є–і–±–∞—О—В—М –љ–∞ —А–Є–љ–Ї—Г, –Ј–∞–ї–µ–ґ–Є—В—М –≤—Ц–і —Ж—Ц–љ–Є –љ–∞ —Ж–µ–є —В–Њ–≤–∞—А. –°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Ж—Ц–љ–Њ—О –є –Ї—Ц–ї—М–Ї—Ц—Б—В—О –Ї—Г–њ–ї–µ–љ–Њ–≥–Њ —В–Њ–≤–∞—А—Г –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —Д—Г–љ–Ї—Ж—Ц—Ф—О –∞–±–Њ –Ј–∞–Ї–Њ–љ–Њ–Љ –њ–Њ–њ–Є—В—Г.
–Ъ—Ц–ї—М–Ї—Ц—Б—В—М —В–Њ–≤–∞—А—Г, —Й–Њ –≤–Є—А–Њ–±–љ–Є–Ї–Є –≤–Є—Б—В–∞–≤–ї—П—В—М –љ–∞ –њ—А–Њ–і–∞–ґ, —В–∞–Ї–Њ–ґ –Ј–∞–ї–µ–ґ–Є—В—М –≤—Ц–і —Ж—Ц–љ–Є –љ–∞ —Ж–µ–є —В–Њ–≤–∞—А. –°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Ж—Ц–љ–Њ—О –є –Ї—Ц–ї—М–Ї—Ц—Б—В—О —В–Њ–≤–∞—А—Г, –≤–Є—Б—В–∞–≤–ї–µ–љ–Њ–≥–Њ –љ–∞ –њ—А–Њ–і–∞–ґ, –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —Д—Г–љ–Ї—Ж—Ц—Ф—О –∞–±–Њ –Ј–∞–Ї–Њ–љ–Њ–Љ –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—Ч.
–£ –љ–∞–є–њ—А–Њ—Б—В—Ц—И–Њ–Љ—Г –≤–Є–њ–∞–і–Ї—Г —Ж—Ц —Д—Г–љ–Ї—Ж—Ц—Ч —Ф –ї—Ц–љ—Ц–є–љ–Є–Љ–Є (—А–Є—Б. 3).
 
 
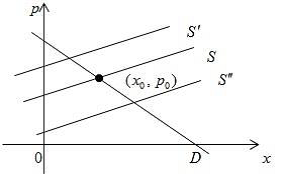
 
–†–Є—Б. 3.
¬†–Ч–∞–Ї–Њ–љ –њ–Њ–њ–Є—В—Г –њ–Њ–Ј–љ–∞—З–µ–љ–Є–є —З–µ—А–µ–Ј \(D\), –Ј–∞–Ї–Њ–љ –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—Ч ¬†вАУ —З–µ—А–µ–Ј \(S\) ;
\(x\) вАУ –Ї—Ц–ї—М–Ї—Ц—Б—В—М —В–Њ–≤–∞—А—Г, \(p\) вАУ —Ж—Ц–љ–∞ –љ–∞ —Ж–µ–є —В–Њ–≤–∞—А.
–†—Ц–≤–љ—П–љ–љ—П –њ–Њ–њ–Є—В—Г –Љ–Њ–ґ–љ–∞ —Б–Ї–ї–∞—Б—В–Є, —П–Ї—Й–Њ –Ј–∞–і–∞–љ—Ц –і–≤—Ц —В–Њ—З–Ї–Є, —Й–Њ –ї–µ–ґ–∞—В—М –љ–∞ –є–Њ–≥–Њ –≥—А–∞—Д—Ц–Ї—Г. –Ф–ї—П —Ж—М–Њ–≥–Њ –њ–Њ—В—А—Ц–±–љ–Њ –≤–Є–Ї–Њ—А–Є—Б—В–∞—В–Є —А—Ц–≤–љ—П–љ–љ—П –њ—А—П–Љ–Њ—Ч,—Й–Њ –њ—А–Њ—Е–Њ–і–Є—В—М —З–µ—А–µ–Ј –і–≤—Ц –Ј–∞–і–∞–љ—Ц —В–Њ—З–Ї–Є.
–Ґ–Њ—З–Ї–∞ –њ–µ—А–µ—В–Є–љ–∞–љ–љ—П –Ї—А–Є–≤–Є—Е –њ–Њ–њ–Є—В—Г —В–∞ –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—Ч \(x_0\), \(p_0\) ¬†–љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —В–Њ—З–Ї–Њ—О —А–Є–љ–Ї–Њ–≤–Њ—Ч —А—Ц–≤–љ–Њ–≤–∞–≥–Є.¬†
–Т—Ц–і–њ–Њ–≤—Ц–і–љ–Њ,¬†
\(p_0\) ¬†- –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —А—Ц–≤–љ–Њ–≤–∞–ґ–љ–Њ—Ч —Ж—Ц–љ–Њ—О,¬†
\(x_0\) ¬†вАУ ¬†—А—Ц–≤–љ–Њ–≤–∞–ґ–љ–Њ—О –Ї—Ц–ї—М–Ї—Ц—Б—В—О (—А—Ц–≤–љ–Њ–≤–∞–ґ–љ–Є–Љ –Њ–±—Б—П–≥–Њ–Љ –њ—А–Њ–і–∞–ґ—Ц–≤).
–С—Г–≤–∞—Ф, —Й–Њ —Г—А—П–і –≤–≤–Њ–і–Є—В—М –њ–Њ–і–∞—В–Њ–Ї t–љ–∞ —В–Њ–≤–∞—А –∞–±–Њ –љ–∞–і–∞—Ф —Б—Г–±—Б–Є–і—Ц—О s, —Й–Њ–± –љ–∞—Б–µ–ї–µ–љ–љ—П –Љ–Њ–≥–ї–Њ –њ—А–Є–і–±–∞—В–Є —В–Њ–≤–∞—А –њ–Њ —А–Њ–Ј—Г–Љ–љ—Ц–є —Ж—Ц–љ—Ц.
–Я—А–Є –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—Ц –ї—Ц–љ—Ц–є–љ–Є—Е –Љ–Њ–і–µ–ї–µ–є –њ–µ—А–µ–і–±–∞—З–∞—Ф—В—М—Б—П, —Й–Њ –њ–Њ–њ–Є—В –≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П —В—Ц–ї—М–Ї–Є —Ж—Ц–љ–Њ—О —В–Њ–≤–∞—А—Г –љ–∞ —А–Є–љ–Ї—Г pc , –∞ –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—П ¬† ћґ ¬†—В—Ц–ї—М–Ї–Є —Ж—Ц–љ–Њ—О ps, —П–Ї—Г –Њ—В—А–Є–Љ—Г—О—В—М –њ–Њ—Б—В–∞—З–∞–ї—М–љ–Є–Ї–Є. –¶—Ц —Ж—Ц–љ–Є –њ–Њ–≤'—П–Ј–∞–љ—Ц –Љ—Ц–ґ —Б–Њ–±–Њ—О –љ–∞—Б—В—Г–њ–љ–Њ—О —Б–Є—Б—В–µ–Љ–Њ—О —А—Ц–≤–љ—П–љ—М : ¬†$$ pc=ps+t \quad pc = ps-s$$ –і–µ \(t\) –є \(s\) ¬† ћґ ¬†–≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ –њ–Њ–і–∞—В–Њ–Ї —В–∞ —Б—Г–±—Б–Є–і—Ц—П –љ–∞ –Њ–і–Є–љ–Є—Ж—О —В–Њ–≤–∞—А—Г.
–Ґ–∞–Ї–Є–Љ —З–Є–љ–Њ–Љ, –њ—А–Є –≤–≤–µ–і–µ–љ–љ—Ц –њ–Њ–і–∞—В–Ї—Г –∞–±–Њ —Б—Г–±—Б–Є–і—Ц—Ч —А—Ц–≤–љ—П–љ–љ—П –њ–Њ–њ–Є—В—Г D –љ–µ –Ј–Љ—Ц–љ–Є—В—М—Б—П. –У—А–∞—Д—Ц–Ї —Д—Г–љ–Ї—Ж—Ц—Ч –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—Ч –њ—Ц–і–љ—Ц–Љ–µ—В—М—Б—П –љ–∞ t–Њ–і–Є–љ–Є—Ж—М –≤–≥–Њ—А—Г (–ї—Ц–љ—Ц—П S¬Ґ) –∞–±–Њ –Њ–њ—Г—Б—В–Є—В—М—Б—П –љ–∞ s–Њ–і–Є–љ–Є—Ж—М —Г–љ–Є–Ј (–ї—Ц–љ—Ц—П S¬Ґ¬Ґ) (–і–Є–≤. —А–Є—Б. 3).
–Ф–µ—П–Ї—Ц –њ–Њ–і–∞—В–Ї–Є, –љ–∞–њ—А–Є–Ї–ї–∞–і –Я–Ф–Т (–њ–Њ–і–∞—В–Њ–Ї –љ–∞ –і–Њ–і–∞–љ—Г –≤–∞—А—В—Ц—Б—В—М), –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц —Ж—Ц–љ—Ц. –£ —Ж—М–Њ–Љ—Г –≤–Є–њ–∞–і–Ї—Г —В–Њ—З–Ї–∞ –њ–µ—А–µ—В–Є–љ—Г –≥—А–∞—Д—Ц–Ї–∞ –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—Ч S –Ј –≤—Ц—Б—Б—О Ox–Ј–∞–ї–Є—И–∞—Ф—В—М—Б—П —В—Ц—Ф—О –ґ, –∞–ї–µ –Љ—Ц–љ—П—Ф—В—М—Б—П –Ї—Г—В –љ–∞—Е–Є–ї—Г –≥—А–∞—Д—Ц–Ї–∞ –і–Њ –Њ—Б—Ц Ox .
–Ч–∞–і–∞—З–∞ 2.(–і.–Ј.) –Ч–∞–Ї–Њ–љ–Є –њ–Њ–њ–Є—В—Г —В–∞ –њ—А–Њ–њ–Њ–Ј–Є—Ж—Ц—Ч –љ–∞ –і–µ—П–Ї–Є–є —В–Њ–≤–∞—А –≤–Є–Ј–љ–∞—З–∞—О—В—М—Б—П —А—Ц–≤–љ—П–љ–љ—П–Љ–Є p=-2x+12+m+n —В–∞ p=x+3+m+n ¬†–≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ, –і–µ m =2 , n ¬†=20
–Ч–∞–≤–і–∞–љ–љ—П.
1) –Ч–љ–∞–є—В–Є —В–Њ—З–Ї—Г —А–Є–љ–Ї–Њ–≤–Њ—Ч —А—Ц–≤–љ–Њ–≤–∞–≥–Є.¬†
2) –Ч–љ–∞–є—В–Є —В–Њ—З–Ї—Г —А—Ц–≤–љ–Њ–≤–∞–≥–Є –њ—Ц—Б–ї—П –≤–≤–µ–і–µ–љ–љ—П –њ–Њ–і–∞—В–Ї—Г, —А—Ц–≤–љ–Њ–≥–Њ 3 –≥—А–љ. –љ–∞ –Њ–і–Є–љ–Є—Ж—О
–њ—А–Њ–і—Г–Ї—Ж—Ц—Ч.
–∞) –Ч–љ–∞–є—В–Є –Ј–±—Ц–ї—М—И–µ–љ–љ—П —Ж—Ц–љ–Є –є –Ј–Љ–µ–љ—И–µ–љ–љ—П —А—Ц–≤–љ–Њ–≤–∞–ґ–љ–Њ–≥–Њ –Њ–±—Б—П–≥—Г –њ—А–Њ–і–∞–ґ—Ц–≤.
–±) –Ч–љ–∞–є—В–Є –і–Њ—Е—Ц–і –і–µ—А–ґ–∞–≤–Є –њ—Ц—Б–ї—П –≤–≤–µ–і–µ–љ–љ—П —Ж—М–Њ–≥–Њ –њ–Њ–і–∞—В–Ї—Г.
3) –ѓ–Ї–∞ —Б—Г–±—Б–Є–і—Ц—П –њ—А–Є–Ј–≤–µ–і–µ –і–Њ –Ј–±—Ц–ї—М—И–µ–љ–љ—П –Њ–±—Б—П–≥—Г –њ—А–Њ–і–∞–ґ—Ц–≤ –љ–∞ 2 ¬†–Њ–і–Є–љ–Є—Ж—Ц?
–Ч–∞–≤–і–∞–љ–љ—П 1, 2, 3 ¬†–Љ–Њ–ґ–љ–∞ –≤–Є–Ї–Њ–љ—Г–≤–∞—В–Є –Ј–∞ –і–Њ–њ–Њ–Љ–Њ–≥–Њ—О –Ї–Њ–Љ–њвАЩ—О—В–µ—А–∞.
–Ч–∞–і–∞—З–∞ 3. –Ы—Ц–љ—Ц—П –і—А—Г–≥–Њ–≥–Њ –њ–Њ—А—П–і–Ї—Г –Ј–∞–і–∞–љ–∞ —А—Ц–≤–љ—П–љ–љ—П–Љ:
¬†\(—Е^2+—Г^2+4—Е+4=0\)
–Ч–∞–≤–і–∞–љ–љ—П.
1) –Я–Њ–±—Г–і–Њ–≤–Њ—О –ї—Ц–љ—Ц—Ч –і—А—Г–≥–Њ–≥–Њ –њ–Њ—А—П–і–Ї—Г, –≤–Є–Ј–љ–∞—З–Є—В–Є –≤–Є–і –ї—Ц–љ—Ц—Ч(–Ї–Њ–ї–Њ, –µ–ї—Ц–њ—Б, –≥—Ц–њ–µ—А–±–Њ–ї–∞ —В–∞ —Ц–љ—И.).
2) –Ч–љ–∞–є—В–Є –Ї–∞–љ–Њ–љ—Ц—З–љ–µ —А—Ц–≤–љ—П–љ–љ—П –ї—Ц–љ—Ц—Ч –і—А—Г–≥–Њ–≥–Њ –њ–Њ—А—П–і–Ї—Г.
–Ч–∞–≤–і–∞–љ–љ—П 1 ¬†–≤–Є–Ї–Њ–љ—Г–≤–∞—В–Є –Ј–∞ –і–Њ–њ–Њ–Љ–Њ–≥–Њ—О–Ї–Њ–Љ–њвАЩ—О—В–µ—А–∞.
 
 
 

