Завдання: Розв'яжіть нерівність \(\frac{10^x-16*5^x}{x+2} \geq 0\). У відповідність запишіть суму всіх цілих розв'язків нерівності на проміжку \([-3;7]\).
Рішення: решим неравенство методом змейки $$\frac{10^x-16*5^x}{x+2} \geq 0 => \begin{cases}(10^x-16*5^x)(x+2) \geq 0\\ x+2 \ne 0\end{cases} => $$$$ \begin{cases}((2*5)^x-16*5^x)(x+2) \geq 0\\ x \ne -2\end{cases} => \begin{cases}(2^x*5^x-16*5^x)(x+2) \geq 0\\ x \ne -2\end{cases} => $$$$ \begin{cases}5^x(2^x-16)(x+2) \geq 0\\ x \ne -2 \end{cases} => \begin{cases}(2^x-2^4)(x+2) \geq 0\\ x \ne -2 \end{cases} => $$область значения показательной функции \(5^x > 0\)$$ \begin{cases}(x-4)(x+2) \geq 0\\ x \ne -2 \end{cases}$$
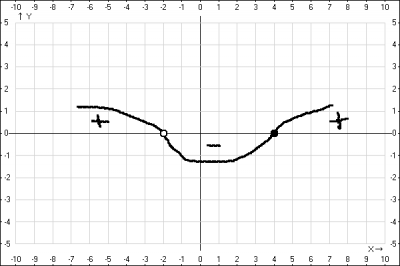
строим змейку, учитываем \(x \ne -2\), получаем ответ \(x \in (-\infty;-2) \cup [4;+\infty)\). В условии дан интервал \([-3;7]\). Ищем пересечения этих интервалов и находим все целые числа: \(-3;4;5;6;7\). Находим сумму полученных чисел: \(-3+4+5+6+7= 19\)

строим змейку, учитываем \(x \ne -2\), получаем ответ \(x \in (-\infty;-2) \cup [4;+\infty)\). В условии дан интервал \([-3;7]\). Ищем пересечения этих интервалов и находим все целые числа: \(-3;4;5;6;7\). Находим сумму полученных чисел: \(-3+4+5+6+7= 19\)
Відповідь: \(19\).
попереднє завдання № 29 наступне завдання № 31
Темы:
математика, зно, зно з математики, зно 2014, ,

