Завдання: Установіть відповідність між функцією \((1-4)\) та кількістю спільних точок \((А - Д)\)графіка цієї функції є графіком функції \(y = \frac{x}{5}\)
Варіант відповіді:
$$\begin{array}{|c|c|c|} \hline 1.\quad y=x+5 & &А.\quad \text{жодної} \\ \hline 2.\quad y=5^x & &Б.\quad \text{лише одна} \\ \hline 3.\quad y=\sqrt{x} & & В.\quad \text{лише дві} \\ \hline 4.\quad y=\sin(x) & &Г. \text{лише три} \\ \hline & &Д. \quad \text{лише чотири} \\ \hline \end{array}$$
Рішення: для решения задания, будем строить графики функция или решать уравнения:
1. функции \(y = \frac{x}{5}\) и \(y=x+5\) , определим количество общих точек.. Если вспомнить свойства прямых на плоскости - у параллельных прямых равны угловые коэффициенты, в данном случае \(k_1=1; k_2=\frac{1}{5} => k_1 \ne k_2\), т.е прямые пересекаются и имеют одну общую точку. Составим уравнение, если прямые имеют общие точки, т.е. равные координаты, приравняем два уравнения \(x+5 = \frac{x}{5} => x = -\frac{25}{4}\), получили одну общую точку. Решим графическим методом. Построим кривые по точкам: 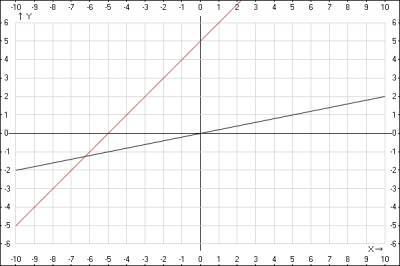
Получили одну общую точку.
Ответ: \(1 \to Б\)
2. функции \(y = \frac{x}{5}\) и \(y = 5^x\), определим количество общих точек. Будем решать графическим методом. Построим кривые по точкам, получаем 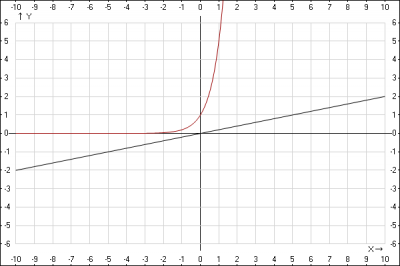
Общих точек нет.
Ответ: \(2 \to А\)
3. функции \(y = \frac{x}{5}\) и \(y=\sqrt{5}\) , определим количество общих точек.. Составим уравнение, если две кривые имеют общие точки, то должно быть решение уравнения, приравняем два уравнения \( \frac{x}{5} = \sqrt{x} => x_1 = 0; x_2=25\). Получили две общие точки. Решение также можно найти графическим методом, строим графики то точкам:
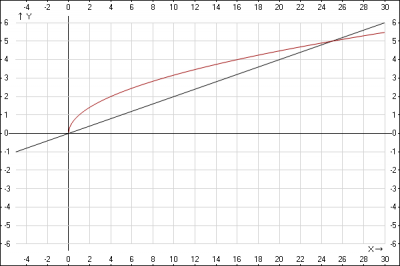
Получили две общие точки.
Ответ: \(3 \to В\)
4. функции \(y = \frac{x}{5}\) и \(y=\sin(x)\) , определим количество общих точек.. Найдем решение графическим методом, строим графики то точкам: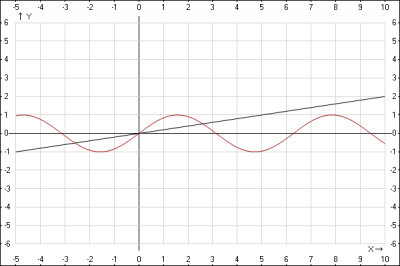
Получили 3 общие точки
Ответ: \(4 \to Д\)
Відповідь: $$\begin{array}{|c|c|c|}\hline & А & Б & В & Г & Д\\ \hline 1& & X & & \\ \hline 2& X & & & \\ \hline 3& & & X & \\ \hline 4& & & & X & \\ \hline \end{array}$$
попереднє завдання № 21 наступне завдання № 23

