–Ч–∞–≤–і–∞–љ–љ—П:¬†–Т–µ–Ї—В–Њ—А \(\vec{OA}\) –ї–µ–ґ–Є—В—М –љ–∞ –Њ—Б—Ц \(z\) –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ—Ч –і–µ–Ї–∞—А—В–Њ–≤–Њ—Ч —Б–Є—Б—В–µ–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В —Г –њ—А–Њ—Б—В–Њ—А—Ц (–і–Є–≤.—А–Є—Б—Г–љ–Њ–Ї), —Ц –є–Њ–≥–Њ –њ–Њ—З–∞—В–Њ–Ї –Ј–±—Ц–≥–∞—Ф—В—М—Б—П –Ј –њ–Њ—З–∞—В–Ї–Њ–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В. –Т–Є–Ј–љ–∞—З—В–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є –≤–µ–Ї—В–Њ—А–∞ \(\vec{OA}\), —П–Ї—Й–Њ –є–Њ–≥–Њ –і–Њ–≤–ґ–Є–љ–∞ –і–Њ—А—Ц–≤–љ—О—Ф 3.¬†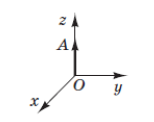
–Т–∞—А—Ц–∞–љ—В –≤—Ц–і–њ–Њ–≤—Ц–і—Ц:
$$\begin{array}{|c|c|c|c|c|} ¬† –Р &–С & –Т & –У & –Ф \\ \hline \\ (1;1;1) & (0;3;0) & (0;0;3) & (3;0;0) & (3;3;3) ¬†\end{array}$$
–†—Ц—И–µ–љ–љ—П:¬†¬†–і–ї–Є–љ–∞ –≤–µ–Ї—В–Њ—А–∞ (–Љ–Њ–і—Г–ї—М –≤–µ–Ї—В–Њ—А–∞) \(a = {a_x ; a_y ; a_z}\) ¬†–і–ї—П –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Л—Е –Ј–∞–і–∞—З –љ–∞—Е–Њ–і–Є—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$|a| = \sqrt{a_x^2 + a_y^2 + a_z^2}$$
–°–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞–љ–Є—П:
1. \(|a| = 3\)
2. –≤–µ–Ї—В–Њ—А \(\vec{OA}\) –ї–µ–ґ–Є—В –љ–∞ –Њ—Б–Є \(z\), —В.–µ. –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ \(\vec{OA} = (0;0;x)\)¬†
–Т—Л–±–Є—А–∞–µ–Љ –њ–Њ–і—Е–Њ–і—П—Й–Є–є –Њ—В–≤–µ—В - –У. –Я—А–Њ–≤–µ—А—П–µ–Љ, –љ–∞–є–і–µ–Љ –і–ї–Є–љ—Г –≤–µ–Ї—В–Њ—А–∞ $$|a| = \sqrt{a_x^2 + a_y^2 + a_z^2} = \sqrt{0^2 + 0^2 + 3^2}=3$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: \(–Т\)
¬†¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 2¬†¬†¬†¬†¬†–љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 4

