–Ч–∞–≤–і–∞–љ–љ—П: –Я–ї–Њ—Й–∞ —А–Њ–Љ–±–∞ –і–Њ—А—Ц–≤–љ—О—Ф \(10,8 \text{ —Б–Љ}^3\), –∞ –њ–ї–Њ—Й–∞ –Ї—А—Г–≥–∞, –≤–њ–Є—Б–∞–љ–Њ–≥–Њ –≤ —Ж–µ–є —А–Њ–Љ–± - \(2,25\pi \text{ —Б–Љ}^2\).
1. –Т–Є–Ј–љ–∞—З—В–µ –і–Њ–≤–ґ–Є–љ—Г —А–∞–і—Ц—Г—Б–∞ –Ї—А—Г–≥–∞, –≤–њ–Є—Б–∞–љ–Њ–≥–Њ –≤ —А–Њ–Љ–± (—Г —Б–Љ).
–†—Ц—И–µ–љ–љ—П:¬†
–Я–ї–Њ—Й–∞–і—М –Ї—А—Г–≥–∞ —А–∞—Б—Б—З–Є—В—Л–≤–∞–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$S_{–Ї—А} = \pi r^2$$ –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –і–∞–љ–љ—Л–µ –Ј–∞–і–∞–љ–Є—П –≤ —Д–Њ—А–Љ—Г–ї—Г $$2,25 \pi = \pi r^2 => r = 1,5$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: $$\begin{array}{|c|c|c|}\hline & & & 1& , &5 & & \\ \hline \hline \end{array} $$
2. –Ю–±—З–Є—Б–ї—Ц—В—М –і–Њ–≤–ґ–Є–љ—Г —Б—В–Њ—А–Њ–љ–Є —А–Њ–Љ–±–∞ (—Г —Б–Љ).
–†—Ц—И–µ–љ–љ—П:¬†
–Я–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞ —А–∞—Б—Б—З–Є—В—Л–≤–∞–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$S_{—А–Њ–Љ–±} = a*h$$
–≥–і–µ \(a\) - —Б—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞
\(h\) - –≤—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–Є—Б—Г–љ–Њ–Ї. 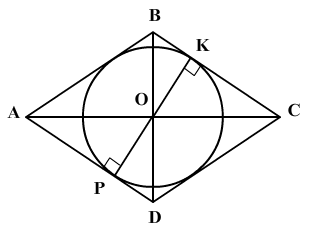
–Ш–Ј —А–Є—Б—Г–љ–Ї–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –≤—Л—Б–Њ—В–∞ \(h = PK = 2r\).¬† –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Д–Њ—А–Љ—Г–ї—Г –њ–ї–Њ—Й–∞–і–Є —А–Њ–Љ–±–∞ $$S_{—А–Њ–Љ–±} = a*2r => a = \frac{S_{—А–Њ–Љ–±}}{2r} = \frac{10,8 \text{ —Б–Љ}^3}{2*1,5 \text{ —Б–Љ}^2} = 3,6 \text{ —Б–Љ}$$ ¬†¬†¬†¬†¬†
–Т—Ц–і–њ–Њ–≤—Ц–і—М: $$\begin{array}{|c|c|c|}\hline & &¬† & 3& , &6 & & \\ \hline \hline \end{array} $$
¬† –њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 25 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 27

