Завдання: На рисунку зображено графік функції \(y = f(x)\), визначеної на відрізку \([-2;6]\). Установіть відповідність між твердженням \((1-4)\) та рівнянням прямої \((А-Д)\), для якої це твердження є правильним.
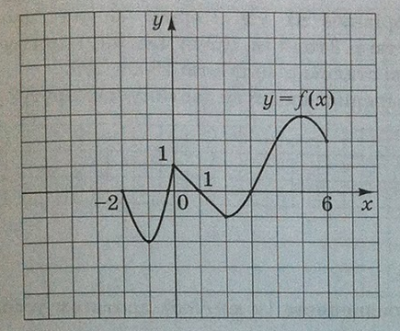
Твердження:
$$\begin{array}{|c|c|c|}\hline \text{1. пряма не перетинає графік функції \(y = f(x)\)} & &А. \quad y = 3+x \\ \hline \text{2. пряма є дотичною, проведеною до графіка функції \(y = f(x)\) у точці з абсцисою \(x = 5\)}& & Б. \quad y = 1 \\ \hline \text{3. пряма перетинає графік функції \(y = f(x)\) у точці з абсцисою \(x = 3\)} & & В. \quad y = 1 - x \\ \hline \text{4. пряма має з графіком функції \(y = f(x)\) не менше трьох спільних точок на відрізку \([0;2]\)}& & Г. \quad y = 3 \\ \hline & & Д. \quad y = 3 - x \\ \hline \end{array}$$
Рішення:
Для установления соответствия нанесем прямые на декартовую систему координат: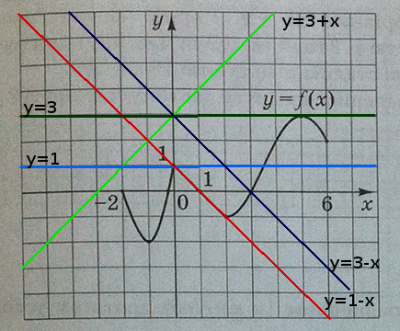
1. пряма не перетинає графік функції \(y = f(x)\)
Согласно рисунка, это прямвя \(y = 3+x \) - вариант ответа \(A\)
2. пряма є дотичною, проведеною до графіка функції \(y = f(x)\) у точці з абсцисою \(x = 5\)
Согласно рисунка это прямая \(y = 3\) - вариант ответа \(Г\)
3. пряма перетинає графік функції \(y = f(x)\) у точці з абсцисою \(x = 3\)
Согласно рисунка это прямая \(y = 3-x\) - вариант ответа \(Д\)
4.пряма має з графіком функції \(y = f(x)\) не менше трьох спільних точок на відрізку \([0;2]\)
Согласно рисунка это прямая \(y = 1-x\) - вариант ответа \(В\)
Відповідь: $$\begin{array}{|c|c|c|}\hline & А & Б & В & Г & Д\\ \hline 1& X & & & \\ \hline 2& & & & X \\ \hline 3& & & & & X \\ \hline 4& & & X & & \\ \hline \end{array}$$

