Завдання: Розвяжіть нерівність \(\frac{3}{x-2}+\frac{4}{x} \geq 1\). У відповіді запишіть суму всіх цілих її розвязків.
Рішення: преобразуем неравенство, приведем дроби к общему знаменателю$$\frac{3}{x-2}+\frac{4}{x} \geq 1 => \frac{3}{x-2}+\frac{4}{x} -1 \geq 0 => $$$$\frac{3*x + 4*(x-2) - x*(x-2)}{x(x-2)} \geq 0 => \frac{3*x + 4*x - 8 – x^2 + 2x}{x(x-2)} \geq 0 =>$$$$ \begin{cases}(9*x - 8 – x^2 )x(x-2) \geq 0 \\ x\ne 0 \\ x-2 \ne 0\end{cases} =>\begin{cases}(x^2 – 9*x + 8)x(x-2) \leq 0 \\ x\ne 0 \\ x \ne 2\end{cases} =>$$$$\begin{cases} x(x-1)(x-2)(x-8) \leq 0 \\ x\ne 0 \\ x \ne 2\end{cases} $$Применим метод "змейки" для решения системы неравенств. Нанесем корни многочлена на числовую ось с учетом \(x \ne 0, x \ne 2\), проведем змейку (смотрим рисунок).
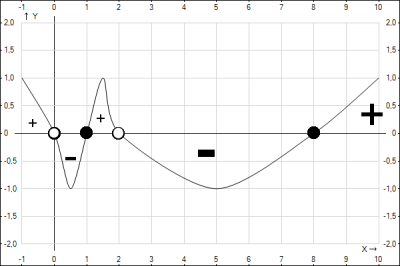
Решением неравенства будут все значения x помеченные "-". Т.о. решением неравенства будет \(x \in (0;1] \cup (2;8]\). Согласно задания, в ответе нужно указать сумму всех целых решений неравенства это будут следующие решения: 1+3+4+5+6+7+8 = 34
Відповідь: 34
Рассмотрим другие варианты этой задачи:
2. Завдання: Розвяжіть нерівність \(\frac{4}{x+3}+\frac{6}{x} \geq 1\). У відповіді запишіть суму всіх цілих її розвязків.
Рішення: $$\frac{4}{x+3}+\frac{6}{x} \geq 1 =>\frac{4}{x+3}+\frac{6}{x} - 1 \geq 0 => $$$$\frac{4*x + 6*(x+3) - x*(x+3)}{x(x+3)} \geq 0 => \frac{4*x + 6*x + 18 - x^2 - 3x}{x(x+3)} \geq 0 =>$$$$ \begin{cases}(7*x + 18 - x^2 )x(x + 3) \geq 0 \\ x\ne 0 \\ x+3 \ne 0\end{cases} =>\begin{cases}(x^2 - 7*x - 18)x(x+3) \leq 0 \\ x\ne 0 \\ x \ne - 3 \end{cases} =>$$$$\begin{cases} x(x+2)(x+3)(x-9) \leq 0 \\ x\ne 0 \\ x \ne -3\end{cases} $$Применим метод "змейки" для решения системы неравенств. Нанесем корни многочлена на числовую ось с учетом \(x \ne 0, x \ne -3\), проведем змейку (смотрим рисунок).
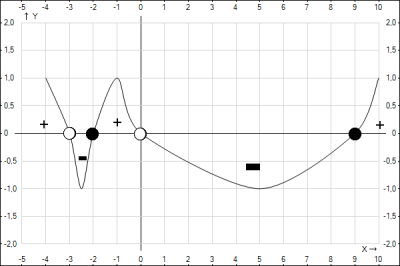
Решением неравенства будут все значения x помеченные "-". Т.о. решением неравенства будет \(x \in (-3;-2] \cup (0;9]\). Согласно задания, в ответе нужно указать сумму всех целых решений неравенства это будут следующие решения: -2+1+2+3+4+5+6+7+8+9 = 43
Відповідь: 43
3. Завдання: Розвяжіть нерівність \(\frac{4}{x-3}+\frac{3}{x} \geq 1\). У відповіді запишіть суму всіх цілих її розвязків.
Рішення: $$\frac{4}{x-3}+\frac{3}{x} \geq 1 =>\frac{4}{x-3}+\frac{3}{x} - 1 \geq 0 => $$$$\frac{4*x + 3*(x-3) - x*(x-3)}{x(x-3)} \geq 0 => \frac{4*x + 3*x - 9 - x^2 + 3x}{x(x-3)} \geq 0 =>$$$$ \begin{cases}(10*x - 9 - x^2 )x(x - 3) \geq 0 \\ x\ne 0 \\ x-3 \ne 0\end{cases} =>\begin{cases}(x^2 - 10*x + 9)x(x-3) \leq 0 \\ x\ne 0 \\ x \ne 3 \end{cases} =>$$$$\begin{cases} x(x-1)(x-3)(x-9) \leq 0 \\ x\ne 0 \\ x \ne 3\end{cases} $$Применим метод "змейки" для решения системы неравенств. Нанесем корни многочлена на числовую ось с учетом \(x \ne 0, x \ne -3\), проведем змейку (смотрим рисунок).
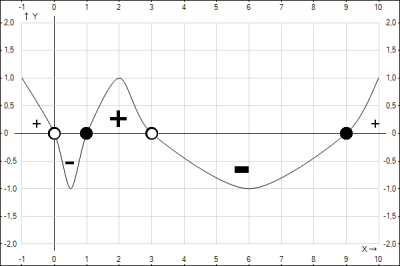
Решением неравенства будут все значения x помеченные "-". Т.о. решением неравенства будет \(x \in (0;1] \cup (3;9]\). Согласно задания, в ответе нужно указать сумму всех целых решений неравенства это будут следующие решения: 1+4+5+6+7+8+9 = 40
Відповідь: 40

