–Ч–∞–≤–і–∞–љ–љ—П: –£—Б—В–∞–љ–Њ–≤—Ц—В—М –≤—Ц–і–њ–Њ–≤—Ц–і–љ—Ц—Б—В—М –Љ—Ц–ґ –Љ–љ–Њ–≥–Њ–Ї—Г—В–љ–Є–Ї–Њ–Љ (1-4) —Ц —А–∞–і—Ц—Г—Б–Њ–Љ –Ї–Њ–ї–∞ (–Р-–Ф), –≤–њ–Є—Б–∞–љ–Њ–≥–Њ –≤ —Ж–µ–є –Љ–љ–Њ–≥–Њ–Ї—Г—В–љ–Є–Ї.
–Ь–љ–Њ–≥–Њ–Ї—Г—В–љ–Є–Ї
- –†—Ц–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ—Ц–є —В—А–Є–Ї—Г—В–љ–Є–Ї –Ј—Ц —Б—В–Њ—А–Њ–љ–Њ—О \(3\sqrt 3 cm\).
- –Ъ–≤–∞–і—А–∞—В –Ј—Ц —Б—В–Њ—А–Њ–љ–Њ—О 2 —Б–Љ.
- –Я—А—П–Љ–Њ–Ї—Г—В–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї —Ц–Ј –Ї–∞—В–µ—В–∞–Љ–Є 6 —Б–Љ —Ц 8 —Б–Љ.
- –Я—А–∞–≤–Є–ї—М–љ–Є–є —И–µ—Б—В–Є–Ї—Г—В–љ–Є–Ї –Ј—Ц —Б—В–Њ—А–Њ–љ–Њ—О 2 —Б–Љ.
–†–∞–і—Ц—Г—Б –Ї–Њ–ї–∞, –≤–њ–Є—Б–∞–љ–Њ–≥–Њ –≤ –Љ–љ–Њ–≥–Њ–Ї—Г—В–љ–Є–Ї
–Р --> 1 —Б–Љ
–С --> 1,5 —Б–Љ
–Т --> \(\sqrt 3\)—Б–Љ
–У --> 2 —Б–Љ
–Ф --> 4 —Б–Љ
¬†–†—Ц—И–µ–љ–љ—П:
- –†—Ц–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ—Ц–є —В—А–Є–Ї—Г—В–љ–Є–Ї –Ј—Ц —Б—В–Њ—А–Њ–љ–Њ—О \(3\sqrt 3 cm\).
–≠—В–Њ—В –≤–Њ–њ—А–Њ—Б –љ–∞ –Ј–љ–∞–љ–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –Ю—Б–љ–Њ–≤–љ–Њ–µ —Б–≤–Њ–є—Б—В–≤–Њ - –≤—Л—Б–Њ—В–∞, –Љ–µ–і–Є–∞–љ–∞, –Є –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ –Њ–і–љ–Њ–є —В–Њ—З–Ї–µ –Є –і–µ–ї—П—В—Б—П –≤ –њ—А–Њ–њ–Њ—А—Ж–Є–Є 2:1, —Б—З–Є—В–∞—П –Њ—В –≤–µ—А—И–Є–љ—Л. –Ґ–Њ—З–Ї–∞ –Є—Е –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П - —Ж–µ–љ—В—А –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї (–Є –Њ–њ–Є—Б–∞–љ–љ–Њ–є) –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.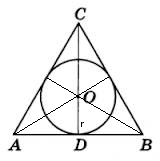
–Р —В–µ–њ–µ—А—М —А–µ—И–µ–љ–Є–µ. –Ш–Ј–≤–µ—Б—В–љ–∞ —Б—В–Њ—А–Њ–љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –Ш–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФDCB\) –љ–∞—Е–Њ–і–Є–Љ \(CD\). –£–≥–Њ–ї \(CBD = 60^0 \), \(\sin(CBD) = \frac{CD}{CB} =>CD = \sin(CBD) * CB\). \(\sin(CBD)=\frac{\sqrt 3}{2}\)¬† \(CB=3\sqrt 3\) $$CD = \sin(CBD) * CB => CD = \frac{\sqrt 3}{2} * 3\sqrt 3 = \frac{9}{2}$$–Ъ–∞–Ї —П —Г–ґ–µ –≥–Њ–≤–Њ—А–Є–ї, –≤ —В–Њ—З–Ї–µ –Ю –Љ–µ–і–Є–∞–љ–∞ \(CD\) –і–µ–ї–Є—В—Б—П –≤ –њ—А–Њ–њ–Њ—А—Ж–Є–Є 2:1, —В.–µ. –љ–∞ 3 —З–∞—Б—В–Є, —В.–µ. $$r = OD = \frac{1}{3}CD = \frac{1}{3} \frac{9}{2} = \frac{3}{2} = 1,5$$
–Х—Б–ї–Є –≤—Б–њ–Њ–Љ–љ–Є—В—М —Д–Њ—А–Љ—Г–ї—Л —В–Њ –њ–Њ–ї—Г—З–Є–Љ —В–Њ—В –ґ–µ —А–µ–Ј—Г–ї—М—В–∞—В. –†–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є \(r = \sqrt {\frac{(p-a)(p-b)(p-c)}{p}}\), –≥–і–µ \(p = \frac{1}{2}(a+b+c)\), —В.–µ. \(a=b=c\) \(p = \frac{1}{2}(a+b+c) = \frac{3}{2}a\). –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Д–Њ—А–Љ—Г–ї—Г —А–∞–і–Є—Г—Б–∞ –Є –њ–Њ–ї—Г—З–∞–µ–Љ \( r = \sqrt {\frac{(p-a)(p-b)(p-c)}{p}} = \sqrt {\frac{(\frac{3}{2}a-a)^2}{\frac{3}{2}a}} = \sqrt{\frac{(\frac{1}{2}a)^3}{\frac{3}{2}a}} =>\) $$r = \frac{a}{2\sqrt 3}$$ –њ–Њ–і—Б—В–∞–≤–Є–Љ –Ј–љ–∞—З–µ–љ–Є–µ —Б—В–Њ—А–Њ–љ—Л \(a = 3\sqrt 3\) –њ–Њ–ї—Г—З–Є–Љ
$$r = \frac{a}{2\sqrt 3} = \frac{3\sqrt 3}{2\sqrt 3} = \frac{3}{2} = 1,5$$ –Х—Б–ї–Є –Ј–∞–њ–Њ–Љ–љ–Є—В–µ —Н—В–Є —Д–Њ—А–Љ—Г–ї—Л, —В–Њ —Н—В–Њ –Ј–∞–Љ–µ—З–∞—В–µ–ї—М–љ–Њ
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 1 -->–С - –Ъ–≤–∞–і—А–∞—В –Ј—Ц —Б—В–Њ—А–Њ–љ–Њ—О 2 —Б–Љ.
–° –Ї–≤–∞–і—А–∞—В–Њ–Љ —Б–Њ–≤—Б–µ–Љ –њ—А–Њ—Б—В–Њ. –†–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ \(r = \frac{a}{2} => r=1\)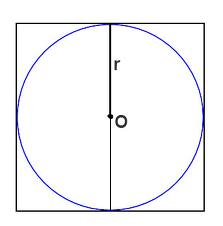
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 2 -->–Р - –Я—А—П–Љ–Њ–Ї—Г—В–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї —Ц–Ј –Ї–∞—В–µ—В–∞–Љ–Є 6 —Б–Љ —Ц 8 —Б–Љ.
–Ф–ї—П —А–µ—И–µ–љ–Є—П —Н—В–Њ–є –Ј–∞–і–∞—З–Є –Љ–Њ–ґ–љ–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Д–Њ—А–Љ—Г–ї
—А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —З–µ—А–µ–Ј –њ–Њ–ї—Г–њ–µ—А–Є–Љ–µ—В—А \(r = \sqrt {\frac{(p-a)(p-b)(p-c)}{p}}\), –≥–і–µ \(p = \frac{1}{2}(a+b+c)\)
$$r = \frac{a+b-c}{2} = \frac{ab}{a+b+c}$$ –і–ї—П –≤—Б–µ—Е —Н—В–Є—Е —Д–Њ—А–Љ—Г–ї –љ—Г–ґ–љ—Л –і–ї–Є–љ—Л –≤—Б–µ—Е —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –Я–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ –љ–∞–є–і–µ–Љ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г \(c = \sqrt {a^2 + b^2} = \sqrt{6^2 + 8^2} = 10 \), –њ–Њ–і—Б—В–∞–≤–Є–Љ –Ј–љ–∞—З–µ–љ–Є–µ –≤ –ї—О–±—Г—О –Є–Ј —Д–Њ—А–Љ—Г–ї –Є –љ–∞–є–і–µ–Љ —А–∞–і–Є—Г—Б $$r = \frac{a+b-c}{2} = \frac{6+8-10}{2} =2$$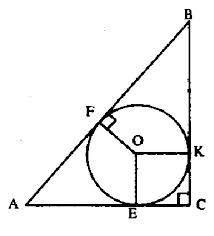
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 3 -->–У - –Я—А–∞–≤–Є–ї—М–љ–Є–є —И–µ—Б—В–Є–Ї—Г—В–љ–Є–Ї –Ј—Ц —Б—В–Њ—А–Њ–љ–Њ—О 2 —Б–Љ.
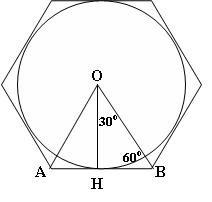
–Э—Г–ґ–љ–Њ –њ–Њ–Љ–љ–Є—В—М, —З—В–Њ –µ—Б–ї–Є –≤–µ—А—И–Є–љ—Г –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б–Њ–µ–і–Є–љ–Є—В—М —Б –≤–µ—А—И–Є–љ–∞–Љ–Є –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –њ–Њ–ї—Г—З–∞—В—Б—П –њ—А–∞–≤–Є–ї—М–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є, –≥–і–µ –≤—Л—Б–Њ—В–∞ \(OH = r\), —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –љ—Г–ґ–љ–Њ –≤—Б–њ–Њ–Љ–љ–Є—В—М —Д–Њ—А–Љ—Г–ї—Г –≤—Л—Б–Њ—В—Л –≤ –њ—А–∞–≤–Є–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ, –∞ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –Є–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ \(ќФOHB\) \(r = OH = OB * \sin (60) =>\) $$ r =\frac{\sqrt{3}}{2}a$$, –≥–і–µ \(a\) - —Б—В–Њ—А–Њ–љ–∞ –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї–∞ (–њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞). –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Є –њ–Њ–ї—Г—З–∞–µ–Љ \(r = 2*\sqrt{3}{2} = \sqrt{3}\)
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 4 -->–Т
–Т—Ц–і–њ–Њ–≤—Ц–і—М:
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 1 -->–С
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 2 -->–Р
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 3 -->–У
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 4 -->–Т
 
 
–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 23 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 25

