–Ч–∞–≤–і–∞–љ–љ—П: –Ю—Б–љ–Њ–≤–Њ—О –њ—А—П–Љ–Њ—Ч –њ—А–Є–Ј–Љ–Є \(ABCDA_1B_1C_1D_1\) —Ф —А–Њ–Љ–± \(ABCD\), —Г —П–Ї–Њ–Љ—Г –±—Ц–ї—М—И–∞ –і—Ц–∞–≥–Њ–љ–∞–ї—М \(AC = 17 cm\). –Ю–±'—Ф–Љ –њ—А–Є–Ј–Љ–Є –і–Њ—А—Ц–≤–љ—О—Ф \(V =1020 cm^3 \). –І–µ—А–µ–Ј –і—Ц–∞–≥–Њ–љ–∞–ї—М \(AC\) —В–∞ –≤–µ—А—И–Є–љ—Г \(B_1\) —В—Г–њ–Њ–≥–Њ –Ї—Г—В–∞ –≤–µ—А—Е–љ—М–Њ—Ч –Њ—Б–љ–Њ–≤–Є –њ—А–Є–Ј–Љ–Є –њ—А–Њ–≤–µ–і–µ–љ–Њ –њ–ї–Њ—Й–Є–љ—Г, —П–Ї–∞ —Г—В–≤–Њ—А—О—Ф –Ј –њ–ї–Њ—Й–Є–љ–Њ—О –Њ—Б–љ–Њ–≤–Є –њ—А–Є–Ј–Љ–Є –Ї—Г—В \(\alpha\). –Ч–љ–∞–є–і—Ц—В—М –њ–ї–Њ—Й—Г —Г—В–≤–Њ—А–µ–љ–Њ–≥–Њ –њ–µ—А–µ—А—Ц–Ј—Г –њ—А–Є–Ј–Љ–Є (—Г \(cm^2\)), —П–Ї—Й–Њ \(\mbox{tg}\alpha = 2,4\)
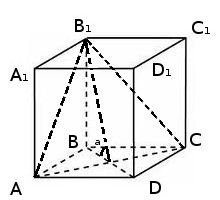
–†—Ц—И–µ–љ–љ—П: –љ–∞—А–Є—Б—Г–µ–Љ —А–Є—Б—Г–љ–Њ–Ї
–Т—Б–њ–Њ–Љ–љ–Є–Љ –Њ—Б–љ–Њ–≤–љ—Л–µ —Д–Њ—А–Љ—Г–ї—Л, –Ї–Њ—В–Њ—А—Л–µ –љ–∞–Љ –њ–Њ–љ–∞–і–Њ–±—П—В—Б—П
- –Ю–±—К–µ–Љ –њ—А—П–Љ–Њ–є –њ—А–Є–Ј–Љ—Л —А–∞–≤–µ–љ \(V = S*H\), –≥–і–µ \(S \) - –њ–ї–Њ—Й–∞–і—М –Њ—Б–љ–Њ–≤–∞–љ–Є—П, \( H\) -–≤—Л—Б–Њ—В–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П —Б –≤–µ—А—Е–љ–µ–≥–Њ –Њ—Б–љ–Њ–≤–∞–љ–Є—П –љ–∞ –љ–Є–ґ–љ–µ–µ. –Ґ.–Ї. –њ—А–Є–Ј–Љ–∞ –њ—А—П–Љ–∞—П, —В–Њ \( H = AA_1=BB_1=CC_1=DD_1\).
- –Я–ї–Њ—Й–∞–і—М –Њ—Б–љ–Њ–≤–∞–љ–Є—П. –Ю—Б–љ–Њ–≤–∞–љ–Є–µ–Љ –њ—А–Є–Ј–Љ—Л —П–≤–ї—П–µ—В—Б—П —А–Њ–Љ–±. –Т —Г—Б–ї–Њ–≤–Є–Є –Ј–∞–і–∞—З–Є –і–∞–љ–∞ –і–ї–Є–љ–∞ –Њ–і–љ–Њ–є –і–Є–∞–≥–Њ–љ–∞–ї–Є —А–Њ–Љ–±–∞, –њ–Њ—Н—В–Њ–Љ—Г –њ–Њ–њ—А–Њ–±—Г–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —Д–Њ—А–Љ—Г–ї—Г –њ–ї–Њ—Й–∞–і–Є —А–Њ–Љ–±–∞ –Њ—В –і–≤—Г—Е –µ–µ –і–Є–∞–≥–Њ–љ–∞–ї–µ–є \(S_{ABCD} = \frac{AC*BD}{2}\).
- –Т —Б–µ—З–µ–љ–Є–Є –Љ—Л –њ–Њ–ї—Г—З–Є–ї–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ \(S_{ќФ}= \frac{1}{2}a*h\), –≥–і–µ \(a\) - –Є–Ј–≤–µ—Б—В–љ–∞ –і–Є–∞–≥–Њ–љ–∞–ї—М —А–Њ–Љ–±–∞ \(AC\), –∞ \(h = B_1O\).
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –Њ–±—К–µ–Љ –Љ–Њ–ґ–љ–Њ –≤—Л—А–∞–Ј–Є—В—М –Ї–∞–Ї $$V = S*h = \frac{AC*BD}{2} *H$$
–Э–∞–є–і–µ–Љ \(H\).–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ \( ќФ BB_1O\). –Т —Н—В–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ —Г –љ–∞—Б –Є–Ј–≤–µ—Б—В–µ–љ \(\mbox{tg}\alpha = 2,4\), –њ—А–Є —Н—В–Њ–Љ $$\mbox{tg}\alpha = \frac{BB_1}{BO} = \frac{BB_1}{\frac{BD}{2}} = 2\frac{BB_1}{BD} => $$$$BB_1 = \frac{1}{2}BD\mbox{tg}\alpha\ = \frac{1}{2}BD*\frac{12}{5} = \frac{6}{5}BD => H=BB_1=\frac{6}{5}BD$$–њ–Њ–і—Б—В–∞–≤–Є–Љ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –≤ –Њ–±—К–µ–Љ $$V =\frac{AC*BD}{2} *H = \frac{AC*BD}{2}*\frac{6}{5}BD$$–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –Љ—Л –њ–Њ–ї—Г—З–Є–ї–Є —Д–Њ—А–Љ—Г–ї—Г –Њ–±—К–µ–Љ–∞, –Ј–∞–≤–Є—Б—П—Й—Г—О –Њ—В –Њ–і–љ–Њ–є –љ–µ–Є–Ј–≤–µ—Б—В–љ–Њ–є \(BD\), –љ–∞–є–і–µ–Љ –µ–µ $$V=\frac{AC*BD}{2}*\frac{6}{5}BD=1020 =>\frac{3}{5}*17*BD^2=1020=>BD^2=100 =>BD = 10$$–Ґ–µ–њ–µ—А—М –Њ–њ—П—В—М –≤–µ—А–љ–µ–Љ—Б—П –≤ \( ќФ BB_1O\) –Љ—Л —Г–ґ–µ –њ–Њ–ї—Г—З–Є–ї–Є —Д–Њ—А–Љ—Г–ї—Г –і–ї—П \(H=BB_1=\frac{6}{5}BD = \frac{6}{5}*10=12\). –Ш–Ј —В–Њ–≥–Њ –ґ–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ –љ–∞—Е–Њ–і–Є–Љ \( h = B_1O = \sqrt{BB_1^2+BO^2}=\sqrt{12^2+5^2}=13\). –Т—Б–µ —З—В–Њ –љ—Г–ґ–љ–Њ –і–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –њ–ї–Њ—Й–∞–і–Є —Б–µ—З–µ–љ–Є—П \(ќФ AB_1C \) –µ—Б—В—М, –љ–∞–є–і–µ–Љ –µ–µ $$S_{AB_1C} = \frac{1}{2}AC*B_1O= \frac{1}{2}*17*13 =110,5$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 110,5
–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 31¬†¬†¬†¬†¬†–љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 33

