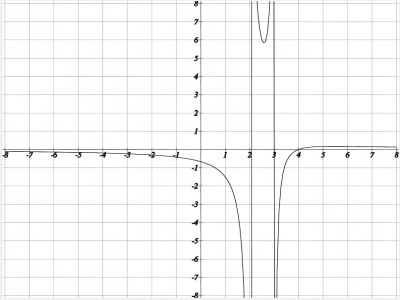
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ–Њ—А—П–і–Њ–Ї –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є –Є –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –µ–µ –≥—А–∞—Д–Є–Ї–∞ –љ–∞ –њ—А–Є–Љ–µ—А–µ —Д—Г–љ–Ї—Ж–Є–Є \(y=\frac{x-4}{(x-3)¬Ј(x-2)}\)
- –Э–∞–є–і–µ–Љ –Њ–±–ї–∞—Б—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є.
–Ю–±–ї–∞—Б—В—М—О –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є \(f(x)\) –љ–∞–Ј—Л–≤–∞—О—В –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –≤—Б–µ—Е –Ј–љ–∞—З–µ–љ–Є–є x , –і–ї—П –Ї–Њ—В–Њ—А—Л—Е —Д—Г–љ–Ї—Ж–Є—П (\(f(x)\)) –Є–Љ–µ–µ—В —Б–Љ—Л—Б–ї. –Т –љ–∞—И–µ–Љ –њ—А–Є–Љ–µ—А–µ —Д—Г–љ–Ї—Ж–Є—П - –і—А–Њ–±—М, –і–ї—П –і—А–Њ–±–Є –Њ–±–ї–∞—Б—В—М—О –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –±—Г–і—Г—В –≤—Б–µ –Ј–љ–∞—З–µ–љ–Є–µ —Е –Ї—А–Њ–Љ–µ —В–µ—Е –њ—А–Є –Ї–Њ—В–Њ—А—Л—Е –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—М —А–∞–≤–µ–љ 0. –Э–∞–є–і–µ–Љ –≤—Б–µ —Е –њ—А–Є –Ї–Њ—В–Њ—А—Л—Е –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—М —А–∞–≤–µ–љ 0. \((x-3)(x-2)=0 =>\) \(x \ne 2\), \(x \ne 3\), —В.–µ –Њ–±–ї–∞—Б—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П \(x \in (-\infty; 2) \cup (2;3) \cup (3;+\infty)\)
–°–і–µ–ї–∞–µ–Љ –њ–µ—А–≤—Л–µ –њ–Њ—Б—В—А–Њ–µ–љ–Є—П - –љ–∞–љ–µ—Б–µ–Љ –љ–∞ –і–µ–Ї–∞—А—В–Њ–≤—Г—О —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В –Њ–±–ї–∞—Б—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П. –Т —В–Њ—З–Ї–∞—Е \(x = 2\), \(x = 3\) –њ–Њ—Б—В—А–Њ–Є–Љ –њ—А—П–Љ—Л–µ \(x = 2\), \(x = 3\) - –њ—А—П–Љ—Л–µ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–µ –Њ—Б–Є \(y\). –≠—В–Є –њ—А—П–Љ—Л–µ –љ–∞–Ј—Л–≤–∞—О—В—Б—П –∞—Б–Є–Љ–њ—В–Њ—В–∞–Љ–Є, –∞–љ–∞–ї–Є–Ј –њ–Њ–≤–µ–і–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є –≤–Њ–Ј–ї–µ –∞—Б–Є–Љ–њ—В–Њ—В –±—Г–і–µ—В –і–∞–ї—М—И–µ. - –Я—А–Њ–≤–µ—А–Є–Љ –љ–∞ —З–µ—В–љ–Њ—Б—В—М —Д—Г–љ–Ї—Ж–Є—О.
–§—Г–љ–Ї—Ж–Є—П¬† \(f\) –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —З—С—В–љ–Њ–є, –µ—Б–ї–Є —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ \(f(x)=f(-x)\)
–§—Г–љ–Ї—Ж–Є—П¬† \(f\) –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –љ–µ—З—С—В–љ–Њ–є, –µ—Б–ї–Є —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ \(f(x)=-f(x)\)
–Я—А–Њ–≤–µ—А—П–µ–Љ –љ–∞ —З–µ—В–љ–Њ—Б—В—М —В.–µ. –≤–Љ–µ—Б—В–Њ \(x\) –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є \(-x\), –њ–Њ–ї—Г—З–Є–Љ: \(\frac{-x-4}{(-x-3)¬Ј(-x-2)}=-\frac{x+4}{(x+3)¬Ј(x+2)} \ne \frac{x-4}{(x-3)¬Ј(x-2)}\), –њ–Њ—Б–ї–µ –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–Є –≤—Л–љ–µ—Б–ї–Є "-" –Ј–∞ —Б–Ї–Њ–±–Ї–Є –Є –њ–Њ–і—Г—З–Є–ї–Є –≤—Л—А–∞–ґ–µ–љ–Є–µ, –Ї–Њ—В–Њ—А–Њ–µ –љ–µ —А–∞–≤–љ–Њ –Є—Б—Е–Њ–і–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є, —В.–µ. –і–∞–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –љ–µ —П–≤–ї—П–µ—В—Б—П –љ–Є —З–µ—В–љ–Њ–є –љ–Є –љ–µ—З–µ—В–љ–Њ–є, –∞ —Н—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ —Г –љ–µ–µ –љ–µ—В —Б–Є–Љ–Љ–µ—В—А–Є–Є –љ–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Њ—Б–Є \(x\) –љ–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —В–Њ—З–Ї–Є O(0;0). - –Э–∞—Е–Њ–і–Є–Љ —Е–∞—А–∞–Ї—В–µ—А–љ—Л–µ —В–Њ—З–Ї–Є –≥—А–∞—Д–Є–Ї–∞.
- –Ґ–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \(x\), —В.–µ. –Ј–љ–∞—З–µ–љ–Є—П \(x\) –њ—А–Є \(y=0\)
$$\frac{x-4}{(x-3)¬Ј(x-2)}=0 => x=4; y=0$$ - –Ґ–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \(y\), —В.–µ. –Ј–љ–∞—З–µ–љ–Є—П \(y\) –њ—А–Є \(x=0\)
$$y=\frac{x-4}{(x-3)¬Ј(x-2)} => y=\frac{0-4}{(0-3)¬Ј(0-2)}=-\frac{2}{3} =>x=0; y=-\frac{2}{3}$$ - –Э–∞–є–і–µ–Љ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–µ —В–Њ—З–Ї–Є (–Є–ї–Є –Ї—А–Є—В–Є—З–µ—Б–Ї–Є–µ —В–Њ—З–Ї–Є) - —В–Њ—З–Ї–Є, –≤ –Ї–Њ—В–Њ—А—Л—Е –≤—Б–µ —З–∞—Б—В–љ—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –Њ–±—А–∞—Й–∞—О—В—Б—П –≤ –љ—Г–ї—М. –Э–∞–є–і–µ–Љ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О –Њ—В —Д—Г–љ–Ї—Ж–Є–Є –Є –њ—А–Є—А–∞–≤–љ—П–µ–Љ –µ–µ –Ї 0.$$(\frac{x-4}{(x-3)(x-2)})`=0 =>( \frac{x-4}{x^2-5x+6})`=0 =>$$$$\frac{(x-4)`(x^2-5x+6)-(x^2-5x+6)`*(x-4)}{(x^2-5x+6)^2}=0 => \frac{x^2-5x+6-(2x-5)(x-4)}{(x^2-5x+6)^2}=0 =>$$$$\frac{x^2-5x+6-(2x^2-13x+20)}{(x^2-5x+6)^2}=0 =>x^2-5x+6-2x^2+13x-20 =0 => $$$$ -x^2+8x-14 = 0 =>x^2-8x+14 = 0 =>$$$$x_{1,2}=\frac{8 \pm \sqrt{64-56}}{2}=\frac{8 \pm \sqrt{8}}{2} = 4 \pm \sqrt{2}=>$$$$x= 4 + \sqrt{2} \approx 5,41; y \approx 0.17$$$$x= 4 - \sqrt{2} \approx 2,59; y \approx 5,83$$–Э–∞–љ–µ—Б–µ–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ —А–µ–Ј—Г–ї—М—В–∞—В—Л –љ–∞ –і–µ–Ї–∞—А—В–Њ–≤—Г—О —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В
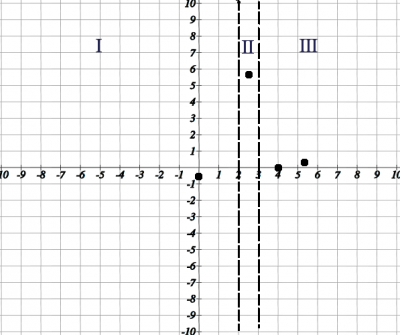
–°—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–µ —В–Њ—З–Ї–Є (—Н–Ї—Б—В—А–µ–Љ—Г–Љ—Л –Є —В–Њ—З–Ї–Є –њ–µ—А–µ–≥–Є–±–∞) –њ–Њ–њ–∞–ї–Є –≤ –Є–љ—В–µ—А–≤–∞–ї—Л \(II - (2;3)\) –Є \(III - (3;+\infty)\). –Ю–њ—А–µ–і–µ–ї–Є–Љ, —П–≤–ї—П—О—В—Б—П —Н—В–Є —В–Њ—З–Ї–Є —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞–Љ–Є (–Љ–∞–Ї—Б–Є–Љ—Г–Љ, –Љ–Є–љ–Є–Љ—Г–Љ) –Є–ї–Є —В–Њ—З–Ї–∞–Љ–Є –њ–µ—А–µ–≥–Є–±–∞.
–Ф–Њ—Б—В–∞—В–Њ—З–љ—Л–Љ —Г—Б–ї–Њ–≤–Є–µ–Љ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П —Н–Ї—Б—В—А–µ–Љ—Г–Љ–Њ–≤ (–Љ–∞–Ї—Б–Є–Љ—Г–Љ, –Љ–Є–љ–Є–Љ—Г–Љ) —П–≤–ї—П–µ—В—Б—П –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Ј–љ–∞–Ї–∞ –њ–µ—А–≤–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –њ—А–Є –њ–µ—А–µ—Е–Њ–і–µ —З–µ—А–µ–Ј —В–Њ—З–Ї—Г —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞.
–Ґ–Њ—З–Ї–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ –Ј–љ–∞–Ї –Љ–µ–љ—П–µ—В—Б—П —Б "+"¬† –љ–∞ "-" (—Д—Г–љ–Ї—Ж–Є—П –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В –і–Њ —В–Њ—З–Ї–Є —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞, –∞ –њ–Њ—Б–ї–µ –љ–µ–µ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В).
–Ґ–Њ—З–Ї–∞ –Љ–Є–љ–Є–Љ—Г–Љ –Ј–љ–∞–Ї –Љ–µ–љ—П–µ—В—Б—П —Б"-" –љ–∞ "+" (—Д—Г–љ–Ї—Ж–Є—П –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В –і–Њ —В–Њ—З–Ї–Є —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞, –∞ –њ–Њ—Б–ї–µ –љ–µ–µ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В).
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–є —В–Њ—З–Ї–Є –≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ –≤–Ј—П—В—М –і–≤–µ —В–Њ—З–Ї–Є (—Б–њ—А–∞–≤–∞ –Є —Б–ї–µ–≤–∞ –Њ—В —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–є —В–Њ—З–Ї–Є), –њ–Њ–і—Б—В–∞–≤–Є—В—М –≤ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О –Є –Њ–њ—А–µ–і–µ–ї–Є—В—М –µ–µ –Ј–љ–∞–Ї.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –љ–∞–Љ–Є —В–Њ—З–Ї–Є - \(x= 4 - \sqrt{2} \approx 2,59; y \approx 5,83\), –њ–Њ–њ–∞–і–∞–µ—В –≤ –Є–љ—В–µ—А–≤–∞–ї \(II\), –њ–Њ—Н—В–Њ–Љ—Г –≤–Њ–Ј—М–Љ–µ–Љ —В–Њ—З–Ї–Є , –љ–∞–њ—А–Є–Љ–µ—А \(x=2.1, x=2,9\). –Ґ–∞–Ї –Ї–∞–Ї –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—М –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –≤—Б–µ–≥–і–∞ –±–Њ–ї—М—И–µ 0, —В–Њ —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —З–Є—Б–ї–Є—В–µ–ї—М \(-x^2+8x-14 \approx -(x-2,59)(x-5,41)\),
–њ–Њ–і—Б—В–∞–≤–Є–Љ \(x=2,1 \quad -(2,1-2,59)(2,1-5,41) < 0\), —В.–µ. "-"
–њ–Њ–і—Б—В–∞–≤–Є–Љ \(x=2,9 \quad -(2,9-2,59)(2,9-5,41) > 0\), —В.–µ. "+"
–Т—Л–≤–Њ–і: –Ј–љ–∞–Ї –Љ–µ–љ—П–µ—В—Б—П —Б"-" –љ–∞ "+" - —В–Њ—З–Ї–∞ –Љ–Є–љ–Є–Љ—Г–Љ–∞ - \(x= 4 + \sqrt{2} \approx 5,41; y \approx 0.17\), –њ–Њ–њ–∞–і–∞–µ—В –≤ –Є–љ—В–µ—А–≤–∞–ї \(III\), –њ–Њ—Н—В–Њ–Љ—Г –≤–Њ–Ј—М–Љ–µ–Љ —В–Њ—З–Ї–Є , –љ–∞–њ—А–Є–Љ–µ—А \(x=5, x=6\). –Ґ–∞–Ї –Ї–∞–Ї –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—М –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –≤—Б–µ–≥–і–∞ –±–Њ–ї—М—И–µ 0, —В–Њ —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —З–Є—Б–ї–Є—В–µ–ї—М \(-x^2+8x-14 \approx -(x-2,59)(x-5,41)\),
–њ–Њ–і—Б—В–∞–≤–Є–Љ \(x=5 \quad -(5-2,59)(5-5,41) > 0\), —В.–µ. "+"
–њ–Њ–і—Б—В–∞–≤–Є–Љ \(x=6 \quad -(6-2,59)(6-5,41) < 0\), —В.–µ. "-"
–Т—Л–≤–Њ–і: –Ј–љ–∞–Ї –Љ–µ–љ—П–µ—В—Б—П —Б"+" –љ–∞ " - " - —В–Њ—З–Ї–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ - –Ш—Б—Б–ї–µ–і—Г–µ–Љ —Д—Г–љ–Ї—Ж–Є—О –љ–∞ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ—Б—В—М
–Ф–Њ—Б—В–∞—В–Њ—З–љ—Л–Љ —Г—Б–ї–Њ–≤–Є–µ–Љ –≤–Њ–Ј—А–∞—Б—В–∞–љ–Є—П¬† (—Г–±—Л–≤–∞–љ–Є—П ) —Д—Г–љ–Ї—Ж–Є–Є —П–≤–ї—П–µ—В—Б—П \(f`(x_0) > 0\) (\(f`(x_0) < 0\)). –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Б–і–µ–ї–∞—В—М –≤—Л–≤–Њ–і –Њ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ—Б—В–Є —Д—Г–љ–Ї—Ж–Є–Є –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ–Њ–і—Б—В–∞–≤–Є—В—М \(x\) –Є–Ј –Њ–±–ї–∞—Б—В–Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П. –Ф–ї—П –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ \(II,III\) –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ—Б—В—М –±—Л–ї–∞ —Г–ґ–µ —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ–∞ –њ—А–Є –∞–љ–∞–ї–Є–Ј–µ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л—Е —В–Њ—З–µ–Ї, —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ—Б—В—М –љ–∞ –Є–љ—В–µ—А–≤–∞–ї–µ \(I\). –Ґ.–Ї. –љ–∞ —Н—В–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ –љ–µ—В —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л—Е —В–Њ—З–µ–Ї, —В–Њ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ—Б—В—М –Љ–µ–љ—П—В—М—Б—П –љ–µ –±—Г–і–µ—В. –Я–Њ–і—Б—В–∞–≤–Є–Љ –Ј–љ–∞—З–µ–љ–Є–µ –ї—О–±–Њ–є —В–Њ—З–Ї–Є \(x\) –Є–љ—В–µ—А–≤–∞–ї–∞ –≤ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О –Є –Њ–њ—А–µ–і–µ–ї–Є–Љ –µ–µ –Ј–љ–∞–Ї. \(x=0, \quad => -(x-2,59)(x-5,41) = -(0-2,59)(0-5,41) < 0 \) - –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \( x \to +\infty \), \( x \to -\infty \), –∞ —В–∞–Ї–ґ–µ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –≤ —А–∞–є–Њ–љ–µ –∞—Б–Є–Љ–њ—В–Њ—В.
- –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x \to -\infty\)
$$\lim_{x \to -\infty}y=\lim_{x \to -\infty}\frac{x-4}{(x-3)¬Ј(x-2)}=\lim_{x \to -\infty}\frac{x-4}{x^2-5x+6} =>$$$$\lim_{x \to -\infty}\frac{1-\frac{4}{x}}{x-5+\frac{6}{x}}=\frac{1-\frac{4}{-\infty}}{-\infty-5+\frac{6}{-\infty}}=\frac{1+0}{-\infty-5-0}=-0$$—В.–Њ. –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї 0 —Б–љ–Є–Ј—Г –њ—А–Є \(x \to -\infty\), —Н—В–Њ—В –ґ–µ —А–µ–Ј—Г–ї—М—В–∞—В –Љ—Л –њ–Њ–ї—Г—З–Є–ї–Є –њ—А–Є –∞–љ–∞–ї–Є–Ј–µ —В–Њ—З–µ–Ї –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \(x\) –Є \(y\). –Э–∞ –і–∞–љ–љ–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ –њ–µ—А–µ—Б–µ—З–µ–љ–Є–є —Б –Њ—Б—М—О \(x\) –љ–µ—В, –∞ —Б \(y=-\frac{2}{3}\) - –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ–µ. - –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x \to +\infty\)
$$\lim_{x \to +\infty}y=\lim_{x \to +\infty}\frac{x-4}{(x-3)¬Ј(x-2)}=\lim_{x \to +\infty}\frac{x-4}{x^2-5x+6} =>$$$$\lim_{x \to +\infty}\frac{1-\frac{4}{x}}{x-5+\frac{6}{x}}=\frac{1-\frac{4}{+\infty}}{+\infty-5+\frac{6}{+\infty}}=\frac{1-0}{+\infty-5+0}=+0$$—В.–Њ. –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї 0 —Б–≤–µ—А—Е—Г –њ—А–Є \(x \to +\infty\), —Н—В–Њ—В –ґ–µ —А–µ–Ј—Г–ї—М—В–∞—В –Љ—Л –њ–Њ–ї—Г—З–Є–ї–Є –њ—А–Є –∞–љ–∞–ї–Є–Ј–µ —В–Њ—З–µ–Ї –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \(x\) –Є \(y\). –Э–∞ –і–∞–љ–љ–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ —Д—Г–љ–Ї—Ж–Є—П –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В –і–Њ —В–Њ—З–Ї–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ \(x= 4 + \sqrt{2} \approx 5,41; y \approx 0.17\), –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –Њ—Б—М \(x=4\), –і–∞–ї–µ–µ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В, –њ—А–Є —Н—В–Њ–Љ –≤—В–Њ—А–Њ–є —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \(x\) –љ–µ—В. - –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x \to 2-0\)
$$\lim_{x \to 2-0}y=\lim_{x \to 2-0}\frac{x-4}{(x-3)¬Ј(x-2)}=\lim_{x \to 2-0}\frac{2-0-4}{(2-0-3)¬Ј(2-0-2)} =>$$$$\frac{-2-0}{(-1-0)¬Ј(-0)}=\frac{-2}{(-1)¬Ј(-0)}=-\infty$$ - –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x \to 2+0\)
$$\lim_{x \to 2+0}y=\lim_{x \to 2+0}\frac{x-4}{(x-3)¬Ј(x-2)}=\lim_{x \to 2+0}\frac{2+0-4}{(2+0-3)¬Ј(2+0-2)} =>$$$$\frac{-2+0}{(-1+0)¬Ј(+0)}=\frac{-2}{(-1)¬Ј(+0)}=+\infty$$ - –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x \to 3-0\)
$$\lim_{x \to 3-0}y=\lim_{x \to 3-0}\frac{x-4}{(x-3)¬Ј(x-2)}=\lim_{x \to 3-0}\frac{3-0-4}{(3-0-3)¬Ј(3-0-2)} =>$$$$\frac{-1-0}{(-0)¬Ј(1-0)}=\frac{-1}{(-0)¬Ј1}=+\infty$$ - –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x \to 3+0\)
$$\lim_{x \to 3+0}y=\lim_{x \to 3+0}\frac{x-4}{(x-3)¬Ј(x-2)}=\lim_{x \to 3+0}\frac{3+0-4}{(3+0-3)¬Ј(3+0-2)} =>$$$$\frac{-1+0}{(+0)¬Ј(1+0)}=\frac{-1}{(+0)¬Ј1}=-\infty$$
- –Ш—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x \to -\infty\)
- –Я–Њ—Б—В—А–Њ–µ–љ–Є–µ –≥—А–∞—Д–Є–Ї–∞ —Д—Г–љ–Ї—Ж–Є–Є.
- –Є–љ—В–µ—А–≤–∞–ї \(-\infty; 2\). –Я—А–Є \(x \to -\infty\) –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї –Њ—Б–Є \(x\). –Я—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є \(x\) –і–Њ \(x \to 2\) –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В, –≤ —В–Њ—З–Ї–µ \(x=0\) –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –Њ—Б—М \(y\) –≤ —В–Њ—З–Ї–µ
–Я–Њ–ї—Г—З–Є–ї–Є —Б–ї–µ–і—Г—О—Й–Є–µ —А–µ–Ј—Г–ї—М—В–∞—В—Л
–љ–∞ \(I\) - —Д—Г–љ–Ї—Ж–Є—П –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В, —В–Њ—З–µ–Ї –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б –Њ—Б—М—О \(x\) –љ–µ—В, –∞ —Б –Њ—Б—М—О \(y=-\frac{2}{3}\), –і–∞–ї–µ–µ –њ—А–Є \(x \to 2\) –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П —Б–ї–µ–≤–∞ –Ї –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–є –∞—Б–Є–Љ–њ—В–Њ—В–µ \(y=2\), —В.–µ. —Д—Г–љ–Ї—Ж–Є—П \(y \to -\infty\). - –Є–љ—В–µ—А–≤–∞–ї \(2; 3\). –Я—А–Є \(x \to 2+0\) —Б–њ—А–∞–≤–∞ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї –њ—А—П–Љ–Њ–є \(x=2, y \to +\infty\). –Я—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є \(x=2 \to x=3\) –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В –і–Њ —В–Њ—З–Ї–Є –Љ–Є–љ–Є–Љ—Г–Љ–∞ \(x= 4 - \sqrt{2} \approx 2,59; y \approx 5,83\), –і–∞–ї–µ–µ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В –Є –њ—А–Є \(x \to 3\) –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї –њ—А–Є–Љ–Њ–є \(x = 3\) \(y \to +\infty\).
- –Є–љ—В–µ—А–≤–∞–ї \(3; +\infty\). –Я—А–Є \(x \to 3+0\) —Б–њ—А–∞–≤–∞ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї –њ—А—П–Љ–Њ–є \(x=3, y \to -\infty\). –Я—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є \(x=3 \to +\infty\) –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В –і–Њ —В–Њ—З–Ї–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ \(x= 4 + \sqrt{2} \approx 5,41; y \approx 0.17\), –њ—А–Є —Н—В–Њ–Љ –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –Њ—Б—М \(x\) –≤ —В–Њ—З–Ї–µ \(x=4\), –і–∞–ї–µ–µ –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В –Є –њ—А–Є \(x \to +\infty\) –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї –Њ—Б–Є \(x\) —Б–≤–µ—А—Е—Г \(y \to +\infty\).
- –Є–љ—В–µ—А–≤–∞–ї \(-\infty; 2\). –Я—А–Є \(x \to -\infty\) –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–∞–µ—В—Б—П –Ї –Њ—Б–Є \(x\). –Я—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є \(x\) –і–Њ \(x \to 2\) –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –Љ–Њ–љ–Њ—В–Њ–љ–љ–Њ —Г–±—Л–≤–∞–µ—В, –≤ —В–Њ—З–Ї–µ \(x=0\) –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –Њ—Б—М \(y\) –≤ —В–Њ—З–Ї–µ
–°—В—А–Њ–Є–Љ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є