Продовжуємо вивчати завдання зно з математики 2012.
Зміст завдання : Прямокутник із сторонами 8 см і 10 см обертається навколо меньшої сторони (див. рисунок). Знайдіть площу повної поверхні отриманого тіла обертання?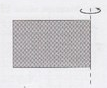
Відповіді до завдання:
А |
Б |
В |
Г |
Д |
\(360\pi см^2\)
|
\(160\pi см^2\) |
\(260\pi см^2\) |
\(288\pi см^2\) |
\(800\pi см^2\) |
Теорія до завдання: Це завдання на об'ємне мислення. Потрібно правильно представити себе фігуру, яка виходить при обертанні. Це буде циліндр.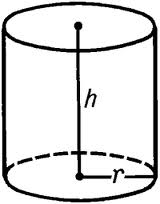
де h = 8 см, це менша сторона навколо якої обертається прямокутник, r = 10 - велика сторона прямокутника
Рішення:
Т.ч. Необхідно знайти площу поверхні циліндра, що дорівнює
1. удвоіной площі підстави - коло радіусом r = 10 см, \(2*S_{осн} = 2 * \pi r^2\).
2. площі бічної поверхні, яка дорівнює площі прямокутника, одна сторона якого - h (висота циліндра), а друга сторона - довжина кола основи - \(2\pi r\) (якщо розрізати бічну сторону циліндра вздовж висоти і розгорнути, то отримаємо вказаний прямокутник)
$$S_{загальне} = 2*S_{осн} + S_{біч.поверхні}$$$$S_{загальне} = 2*\pi r2 + h*2\pi r$$$$S_{загальне} = 2 *\pi * 10^2 + 8 *2*\pi*10 = 200*\pi + 160*\pi = 360\pi $$
Відповідь: А: \(360\pi\).

