–Ч–∞–≤–і–∞–љ–љ—П:¬†–І–µ—А–µ–Ј —В–Њ—З–Ї–Є A —Ц B, —Й–Њ –ї–µ–ґ–∞—В—М –љ–∞ –Ї–Њ–ї–∞—Е –≤–µ—А—Е–љ—М–Њ—Ч —В–∞ –љ–Є–ґ–љ—М–Њ—Ч –Њ—Б–љ–Њ–≤ —Ж–Є–ї—Ц–љ–і—А–∞ —Ц –љ–µ –љ–∞–ї–µ–ґ–∞—В—М –Њ–і–љ—Ц—Ч —В–≤—Ц—А–љ—Ц–є, –њ—А–Њ–≤–µ–і–µ–љ–Њ –њ–ї–Њ—Й–Є–љ—Г –њ–∞—А–∞–ї–µ–ї—М–љ–Њ –Њ—Б—Ц —Ж–Є–ї—Ц–љ–і—А–∞. –Т—Ц–і—Б—В–∞–љ—М –≤—Ц–і —Ж–µ–љ—В—А–∞ –љ–Є–ґ–љ—М–Њ—Ч –Њ—Б–љ–Њ–≤–Є –і–Њ —Ж—Ц—Ф—Ч –њ–ї–Њ—Й–Є–љ–Є –і–Њ—А—Ц–≤–љ—О—Ф 2 —Б–Љ, –∞ –њ–ї–Њ—Й–∞ —Г—В–≤–Њ—А–µ–љ–Њ–≥–Њ –њ–µ—А–µ—А—Ц–Ј—Г - \(60\sqrt{2}—Б–Љ^2\). –Т–Є–Ј–љ–∞—З—В–µ –і–Њ–≤–ґ–Є–љ—Г –≤—Ц–і—А—Ц–Ј–Ї–∞ AB (—Г —Б–Љ), —П–Ї—Й–Њ –њ–ї–Њ—Й–∞ –±—Ц—З–љ–Њ—Ч –њ–Њ–≤–µ—А—Е–љ—Ц —Ж–Є–ї—Ц–љ–і—А–∞ –і–Њ—А—Ц–≤–љ—О—Ф \(20\sqrt{30}\pi —Б–Љ^2\)
–†—Ц—И–µ–љ–љ—П:¬† —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–Є—Б—Г–љ–Њ–Ї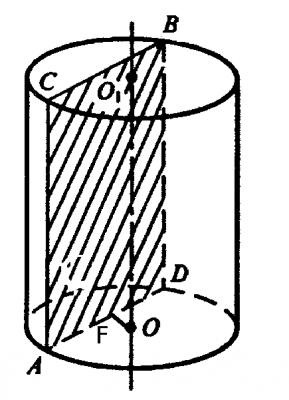 ¬†
 
–Ш—Б–Ї–Њ–Љ—Л–є –Њ—В—А–µ–Ј–Њ–Ї \(AB\) - –і–Є–∞–≥–Њ–љ–∞–ї—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —Б–µ—З–µ–љ–Є—П¬†—Ж–Є–ї–Є–љ–і—А–∞¬†–њ–ї–Њ—Б–Ї–Њ—Б—В—М—О, –Ї–Њ—В–Њ—А–∞—П –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ –Њ—Б–Є —Ж–Є–ї–Є–љ–і—А–∞, –њ–ї–Њ—Й–∞–і—М —Б–µ—З–µ–љ–Є—П –њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є —А–∞–≤–љ–∞ \(S = AC*AD =¬†60\sqrt{2}\).¬†
–Ю—В—А–µ–Ј–Њ–Ї \(AB\) –±—Г–і–µ–Љ –љ–∞—Е–Њ–і–Є—В—М –Є–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ќФABD –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ \(AB = \sqrt{AD^2+BD^2} =¬†\sqrt{AD^2+AC^2}\).¬†
–Э–∞–є–і–µ–Љ —Б—В–Њ—А–Њ–љ—Л \(AC\) –Є \(AD\).
–°–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є –њ–ї–Њ—Й–∞–і—М –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Ж–Є–ї–Є–љ–і—А–∞ —А–∞–≤–љ–∞ \(S_{–±–Њ–Ї} ¬†=20\sqrt{30}\pi\). –Я–ї–Њ—Й–∞–і—М –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Ж–Є–ї–Є–љ–і—А–∞ —А–∞—Б—Б—З–Є—В—Л–≤–∞–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ \(S_{–±–Њ–Ї}¬†= 2\pi RH\) - –≥–і–µ R - —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Њ—Б–љ–Њ–≤–∞–љ–Є—П —Ж–Є–ї–Є–љ–і—А–∞, H - –≤—Л—Б–Њ—В–∞ —Ж–Є–ї–Є–љ–і—А–∞ \(H = AC\). –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –і–∞–љ–љ—Л–µ –≤ —Д–Њ—А–Љ—Г–ї—Г –њ–ї–Њ—Й–∞–і–Є –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є $$ 2\pi R*AC =¬†20\sqrt{30}\pi =>¬†¬†AC*R = 10\sqrt{30}$$ –Т –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї–µ –љ–µ–Є–Ј–≤–µ—Б—В–µ–љ —А–∞–і–Є—Г—Б R. –Э–∞–є–і–µ–Љ –µ–≥–Њ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞¬†ќФAFO –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ $$AF^2+FO^2=AO^2$$ –≥–і–µ AO=R, OF=2, \(AF=\frac{1}{2}AD\), –њ–Њ–ї—Г—З–∞–µ–Љ $$\frac{1}{4}AD^2+4=R^2 $$
–Я–Њ–ї—Г—З–Є–ї–Є —В—А–Є —Г—А–∞–≤–љ–µ–љ–Є—П —Б —В—А–µ–Љ—П –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–Љ–Є, —Б–Њ—Б—В–∞–≤–Є–Љ —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є –Є –љ–∞–є–і–µ–Љ ¬†\(AC\) –Є \(AD\) $$\begin{cases}AC*AD = 60\sqrt{2}\\AC*R = 10\sqrt{30} \\ \frac{1}{4}AD^2+4=R^2 \end{cases}=> \begin{cases}AC =\frac{ 60\sqrt{2}}{AD}\\\frac{ 60\sqrt{2}}{AD}*\sqrt{\frac{1}{4}AD^2+4} = 10\sqrt{30} \\ R = \sqrt{\frac{1}{4}AD^2+4} \end{cases}=> $$$$¬†\begin{cases}AC =\frac{ 60\sqrt{2}}{AD}\\ 6\sqrt{\frac{1}{4}AD^2+4} = \sqrt{15}AD \\ R = \sqrt{\frac{1}{4}AD^2+4} \end{cases}=>¬†\begin{cases}AC =\frac{ 60\sqrt{2}}{AD}\\ 36\frac{1}{4}AD^2+4*36 = 15AD^2 \\ R = \sqrt{\frac{1}{4}AD^2+4} \end{cases}=> $$$$¬†\begin{cases}AC =\frac{ 60\sqrt{2}}{AD}\\ 6AD^2=4*36 \\ R = \sqrt{\frac{1}{4}AD^2+4} \end{cases}=> ¬†\begin{cases}AC =10\sqrt{3}\\ AD=\sqrt{24} \\ R = \sqrt{10} \end{cases}$$
 
–Ш–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ќФABD –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ \(AB = \sqrt{AD^2+BD^2} =¬†\sqrt{AD^2+AC^2}\) $$AB = \sqrt{(\sqrt{24})^2+(10\sqrt{3})^2} = \sqrt{24+300} = 18$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: ¬†–і–Њ–≤–ґ–Є–љ—Г –≤—Ц–і—А—Ц–Ј–Ї–∞ \(AB=18\).
¬†¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 32¬† ¬† ¬†–љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 34
 

