–Ч–∞–≤–і–∞–љ–љ—П:¬†–Ф—Ц–∞–≥–Њ–љ–∞–ї—М —А—Ц–≤–љ–Њ–±—Ц—З–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч —Ф –±—Ц—Б–µ–Ї—В—А–Є—Б–Њ—О —Ч—Ч –≥–Њ—Б—В—А–Њ–≥–Њ –Ї—Г—В–∞ —Ц –і—Ц–ї–Є—В—М —Б–µ—А–µ–і–љ—О –ї—Ц–љ—Ц—О —В—А–∞–њ–µ—Ж—Ц—Ч –љ–∞ –≤—Ц–і—А—Ц–Ј–Ї–Є –і–Њ–≤–ґ–Є–љ–Њ—О 13 —Б–Љ —Ц 23 —Б–Љ. –Ю–±—З–Є—Б–ї—Ц—В—М —Г \((—Б–Љ^2)\) –њ–ї–Њ—Й—Г —В—А–∞–њ–µ—Ж—Ц—Ч.
–†—Ц—И–µ–љ–љ—П:¬†¬†–Я–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є —А–∞—Б—Б—З–Є—В—Л–≤–∞–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$S = \frac{a+b}{2}h = mh \quad (1)$$ –≥–і–µ \(a,b\) - –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є,
\(h\) - –≤—Л—Б–Њ—В–∞ —В—А–∞–њ–µ—Ж–Є–Є.
–Т —В–Њ–ґ–µ –≤—А–µ–Љ—П \(m = \frac{a+b}{2} = 36\) - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
–Ґ.–Њ. –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –љ–∞–є—В–Є –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є –љ—Г–ґ–љ–Њ –љ–∞–є—В–Є –≤—Л—Б–Њ—В—Г —В—А–∞–њ–µ—Ж–Є–Є \(h = AO\).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–Є—Б—Г–љ–Њ–Ї.
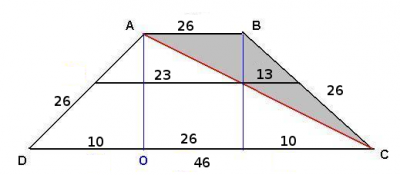
–Ф–ї—П —А–µ—И–µ–љ–Є—П –Ј–∞–і–∞—З–Є –љ—Г–ґ–љ–Њ –љ–∞–є—В–Є –≤—Л—Б–Њ—В—Г AO. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ќФADO. –Т —Н—В–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ AO - –Ї–∞—В–µ—В, –Ї–Њ—В–Њ—А—Л–є –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –њ–Њ —Д–Њ—А–Љ—Г–ї–µ –Я–Є—Д–∞–≥–Њ—А–∞ \(a^2+b^2=c^2\), –Њ—Б—В–∞–ї–Њ—Б—М –љ–∞–є—В–Є –≤—В–Њ—А–Њ–є –Ї–∞—В–µ—В DO –Є –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г AD.
–°—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є —В–∞–Ї–ґ–µ —П–≤–ї—П–µ—В—Б—П —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–µ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ќФABC.
–°–≤–Њ–є—Б—В–≤–∞ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.¬†–°—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —Б–Њ–µ–і–Є–љ—П—О—Й–∞—П —Б–µ—А–µ–і–Є–љ—Л –і–≤—Г—Е –і–∞–љ–љ—Л—Е —Б—В–Њ—А–Њ–љ, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ —В—А–µ—В—М–µ–є —Б—В–Њ—А–Њ–љ–µ –Є —А–∞–≤–љ–∞ –µ–µ –њ–Њ–ї–Њ–≤–Є–љ–µ.¬†
–°–Њ–≥–ї–∞—Б–љ–Њ —Б–≤–Њ–є—Б—В–≤–∞ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ AB = 2*13=26
–°—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є —В–∞–Ї–ґ–µ —П–≤–ї—П–µ—В—Б—П —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–µ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ќФACD.
–°–Њ–≥–ї–∞—Б–љ–Њ —Б–≤–Њ–є—Б—В–≤–∞ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ DC = 2*23=46
–Я–Њ–ї—Г—З–Є–ї–Є –і–ї–Є–љ—Л –Њ—Б–љ–Њ–≤–∞–љ–Є–є —В—А–∞–њ–µ—Ж–Є–Є ¬†\(AB = 26\), \(DC = 46\)
–°–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є: –і–Є–∞–≥–Њ–љ–∞–ї—М —В—А–∞–њ–µ—Ж–Є–Є —П–≤–ї—П–µ—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є –Њ—Б—В—А–Њ–≥–Њ —Г–≥–ї–∞, —В.–µ. \(\angle BCA = \angle ACD\) , –≤ —В–Њ–ґ–µ –≤—А–µ–Љ—П \(\angle ACD = \angle BAC\) —Н—В–Є —Г–≥–ї—Л —А–∞–≤–љ—Л —В.–Ї. —П–≤–ї—П—О—В—Б—П –≤–љ—Г—В—А–µ–љ–љ–Є–Љ–Є –љ–∞–Ї—А–µ—Б—В –ї–µ–ґ–∞—Й–Є–Љ–Є —Г–≥–ї–∞–Љ–Є, —В.–Њ. ¬†\(\angle BCA = \angle ACD = \angle BAC\). –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ ¬†ќФABC - —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є, –∞ —Б—В–Њ—А–Њ–љ—Л \(AB=BC=26\). –Я–Њ–ї—Г—З–Є–ї–Є, —З—В–Њ –±–∞–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є \(AD=BC=26\)
–Э–∞–є–і–µ–Љ –Ї–∞—В–µ—В \(DO = \frac{DC-AB}{2} = \frac{46-26}{2}=10\)
–Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ¬†ќФADO –љ–∞—Е–Њ–і–Є–Љ –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ \(DO=h=\sqrt{AD^2-LJ^2} = \sqrt{26^2-10^2} = 24\)
–Э–∞–є–і–µ–Љ –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є –њ–Њ —Д–Њ—А–Љ—Г–ї–µ (1) $$S = m*h = 36*24 ¬†= 864$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: ¬†–њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ \(864 —Б–Љ^2\).
¬†¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 30¬† ¬† ¬†–љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 32
 

