Завдання: На стороні AD паралелограма ABCD як на діаметрі побудовано півколо так, що воно дотикається до сторони BC в точці M. Довжина дуги MD дорівнює \(6.5 \pi см\).
1. Обчисліть (у см) довжину радіуса цього півкола.
2. Обчисліть площу паралелограма ABCD (у \(см^2\))
Рішення:
Строим рисунок 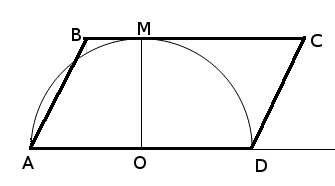
1. Вычислим длину радиуса круга.
Из условия задачи следует, что длина дуги MD равна \(MD=6.6\pi\). Из рисунка видно, что дуга MD - равна четверти длины окружности. Длина окружности рассчитывается по формуле \(l = 2\pi r => MD = \frac{2\pi r}{4} = 6.5\pi => r = 13\)
Ответ: длина радиуса круга равна r = 13 см.
2. Вычислим площадь параллелограмма ABCD.
Площадь параллелограмма будем находить по формуле \(S = ah\), где \(a\) - сторона параллелограмма, \(h\) - высота параллелограмма, опущенная на сторону \(a\)
Сторона параллелограмма \(a = AD = 2r = 26\) согласно условия задачи.
Согласно условия, точка M - точка касания окружности и прямой BC. Радиус, опущенный в точку касания перпендикулярен касательной, т.е. OM - высота, т.е. \(h = OM = r\). Подставляем в формулу площади $$S = ah = 26*13 =338 см^3$$
Ответ: площадь параллелограмма ABCD равна \(S_{ABCD} = 338 см^3\)
Відповідь:
1. длина радиуса круга \(r = 13см\)
2. площадь параллелограмма ABCD равна \(S_{ABCD} = 338 см^3\)
попереднє завдання № 25 наступне завдання № 27

