Завдання: На рисунку зображено квадрат \(ABCD\) зі стороною 1 см та прямокутний трикутник \(CDF\), гіпотенуза якого \(CF\) дорівнює \(\sqrt{5}см\). Фігури лежать в одній площині. Установіть відповідальність між початком речення (1-4) та його закінченням (А-Д) так, щоб утворилося правильне твердження.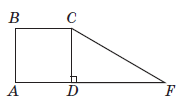
Варіант відповіді:
$$ \begin{array}{|l|c|l|} \hline \quad\quad \large \textbf{Початок речення} & & \large\textbf{Закінчення речення} \\ \hline 1.\quad \text{Довжина катета FD трикутника CDF дорівнює } & &А.\quad \text{1 см} \\ \hline 2.\quad \text{Довжина радіуса кола, описаного навколо квадрата ABCD, дорівнює} & &Б.\quad \frac{1}{\sqrt{2}} см \\ \hline 3.\quad \text{Відстань від точки F до прямої BC дорівнює} & & В.\quad \sqrt{2} см \\ \hline 4.\quad \text{Відстань від точки F до прямої BD дорівнює} & &Г. \quad \text{2 см} \\ \hline & &Д. \quad \sqrt{5} см \\ \hline \end{array}$$
Рішення:
1. Длинна катета FD треугольника CDF равна:
Рассмотрим \(ΔCDF\): известны длина катета \(CD = 1\) и гипотенузы \(CF = \sqrt{5}\), тогда по теореме Пифагора найдем $$CF^6 = CD^2+DF^2 => 5 = 1 + DF^2 => DF=2$$
Ответ: Довжина катета FD трикутника CDF дорівнює 2см, \((1 \to Г)\)
2. Длина радиуса круга, описанного вокруг квадрата:
Если квадрат вписан в круг, то его диагональ является диаметром этого круга. Найдем диагональ из треугольника \(ΔABD\) по теореме Пифагора, согласно условия задачи \(AB=AD=1\), получаем $$AB^2+AD^2 = BD^2 => BD^2 = 1+1 => BD=\sqrt{2} =>d=2r=BD=\sqrt{2} => r = \frac{1}{\sqrt{2}}$$
Ответ: Довжина радіуса кола, описаного навколо квадрата ABCD, дорівнює \( \frac{1}{\sqrt{2}}см\), \((2 \to Б)\)
3. Расстояние от точки F до прямой BC равно :
Расстояние от точки до прямой равно перпендикуляру, опущенному из этой точки на прямую \(FE\). Точка F лежит на прямой AF, которая параллельна BC \(AF||BC\). Все перпендикуляры, опущенные из точек прямой AF на прямую BC равны \(AB=DC=FE=1\), т.е. и перпендикуляр из точки F (FE) на прямую BC равен 1 см.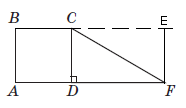
Ответ: Відстань від точки F до прямої BC дорівнює 1 см, \((3 \to А)\)
4. Расстояние от точки F до прямой BD равно :
Опустим перпендикуляр на прямую BD из точки F. Найдем расстояние FS. Из рисунка видно, что углы \(\angle BDA = \angle FDS\). Из прямоугольного равнобедренного треугольника \(ΔABD\) следует, что \(\angle BDA = 45^0 => \angle FDS = 45^0\). Получили, что прямоугольный треугольник \(ΔFDS\) - равнобедренный, т.е. \(DS=SF = a\). Применим теорему Пифагора к этому треугольнике \(DS^2 + SF^2 = DF^2 => a^2+a^2 = 2a^2 = 4 => a=\sqrt{2}\)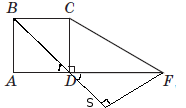
Ответ: Відстань від точки F до прямої BD дорівнює \(\sqrt{2}\) см, \((4 \to В)\)
попереднє завдання № 22 наступне завдання № 24

