Зовнішнє незалежне оцінювання 2012 року з математики (1 сесія). Завдання № 7.

Зміст завдання : Пряма с перетинає паралельні прямі a і b (див. рисунок). Які з наведених тверджень є правильними для кутів 1, 2, 3?

 I   ∠ 1 і ∠ 3 — суміжні.
 II   ∠ 1 = ∠ 2.
 III   ∠2 + ∠3 = \(180^0\).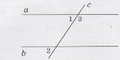

Відповіді до завдання:

Теорія до завдання: Два кути ( ∠1 і ∠2) називаються суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими.

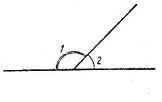
Властивості суміжних кутів:

1. Сума суміжніх кутів дорівнює \(180^0\).


2. Коли два кути рівні, то суміжні з ними кути теж рівні.


3. Кут, суміжний із прямим кутом, є прямий кут.


4. Кут, суміжний із гострим кутом, є тупий кут.


5. Кут, суміжний із тупим кутом, є гострий кут.

Два кути ( ∠1 і ∠3) називаються вертикальними, якщо сторони одного кута є доповняльними півпрямими сторін другого.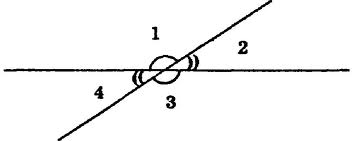



Властивості вертикальних кутів:

1. Вертікальні кути рівні


2. Якщо дві прямі перетинаються, то вони утворюють чотири нерозгорнутих кути (див. рисунок).


3. Кожні два із цих кутів або суміжні, або вертикальні.

Властивості паралельних прямих (див. рисунок):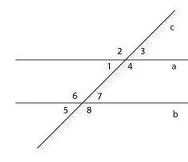



внутрішні різносторонні кути рівні (∠1 = ∠ 7, ∠4 = ∠6).
сума внутрішніх односторонніх кутів дорівнює \(180^0\) (∠1 + ∠6 = \(180^0\)).
зовнішні різностороні кути рівні (∠2 = ∠8, ∠3 = ∠5).
сума зовнішніх односторонніх кутів дорівнює \(180^0\) (∠2+∠5 = \(180^0\)).
відповідні кути рівні (∠2=∠6).

Рішення:

кути ∠1 і ∠3 є суміжними - правильно згідно визначення.
кути ∠1 = ∠2 - правильно, тому що це відповідні кути.
кути ∠2 +∠3 = \(180^0\) - правільно, кути ∠1 і ∠2 є відповіднімі, тобто вони рівні, а кути ∠1 і ∠3 є суміжними, тобто сума кутів ∠1 + ∠3 = \(180^0\), отже, і сума кутів ∠2 + ∠3 = \(180^0\)

Відповідь: Д: І, ІІ та ІІІ.

   попереднє завдання № 6    наступне завдання № 8