Завдання: Об’єм конуса дорівнює \(64 \text{ см}^3\). Через середину висоти цього конуса паралельно його основі проведено площину. Утворений переріз є основою меншого конуса, вершина якого збігається з вершиною заданого. Знайдіть об’єм меншого конуса.
Варіант відповіді:
$$\left|\begin{array}{c}А &Б & В & Г & Д\\
32 \text{ см}^3 & 16 \text{ см}^3 & 12 \text{ см}^3 & 8 \text{ см}^3 & 4 \text{ см}^3 \end{array}\right|$$
Рішення:
Рассмотрим рисунок. 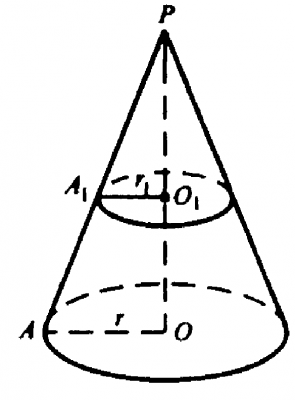
Проведем сечение и рассмотрим два треугольника \(ΔAOP\) и \(ΔAO_1P_1\). Это два подобных реугольника. Коэффициент пропорции \(\frac{A_1P}{AP}= \frac{r_1}{r} = \frac{O_1P}{OP} = \frac{h_1}{h}= \frac{1}{2}\). Воспользуемся формулой объема конуса $$V = \frac{1}{3}S_{осн}h$$ т.к. в основании конуса ледит круг радиуса \(r\), получим $$V = \frac{1}{3}\pi r^2h$$ для искомого конуса известно, что \(r_1 = \frac{1}{2}r\) и \(h_1 = \frac{1}{2}h\), подставляем в формулу обхума конуса, получаем $$V = \frac{1}{3}\pi r_1^2h_1 = \frac{1}{3}\pi (\frac{1}{2}r)^2\frac{h}{2} =$$$$ =\frac{1}{8}(\frac{1}{3}\pi r^2 h) = \frac{1}{8}*64 = 8$$
Відповідь: \(Г\)

